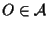5.1 Fissiamo un punto $O\in \mathcal{A}$; affermiamo che l'applicazione

\begin{displaymath}\begin{array}{cclc} f: & \mathcal{A} & \longrightarrow & \mat... ...athsf{a} \\ \; & P & \mapsto & \overrightarrow{OP} \end{array}\end{displaymath}

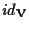è un isomorfismo affine con parte lineare $id_{\mathbf{V}}$:
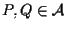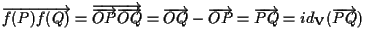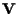Infatti, dati $P,Q \in \mathcal{A}$ abbiamo che $\overrightarrow{f(P)f(Q)}=\overrightarrow{\overrightarrow{OP}\overrightarrow{OQ... ...-\overrightarrow{OP}= \overrightarrow{PQ}=id_{\mathbf{V}}(\overrightarrow{PQ})$ avendo sfruttato la definizione di struttura affine di $\mathbf{V}$ (vedi esempio 5 della sezione "Spazi affini: definizione e proprietà").

Si noti che questa volta non ci serviamo del fatto che 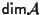$\mathsf{dim}\mathcal{A}$ è finita e in effetti questa dimostrazione vale anche in generale.
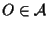Si noti infine che l'isomorfismo esibito non è canonico ma dipende dalla scelta di un punto $O\in \mathcal{A}$, in effetti di questo tipo è anche la corrispondenza tra i punti di piano (o spazio) ordinario e lo spazio dei vettori geometrici applicati appunto in un qualche suo punto.




torna alla teoria