29. Certamente 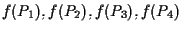sono distinti poiché 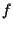è iniettiva.
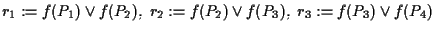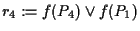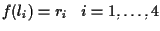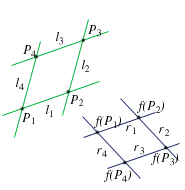
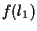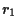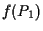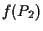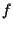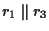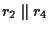Poniamo e . Affermiamo che , infatti ad esempio sia che passano per e . Per ipotesi su si ha quindi che e . Ciò non basta per concludere, infatti 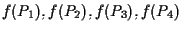potrebbero essere collineari, d'altra parte 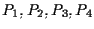non lo sono e quindi, come osservato nella proposizione precedente, si ha che, ad esempio, 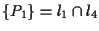da cui ( 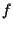iniettiva) 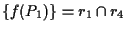che implica 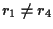e quindi 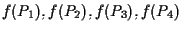non collineari.