22.
Poiché
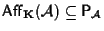 l'insieme di tutte le permutazioni di
l'insieme di tutte le permutazioni di
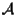 che è gruppo rispetto alla composizione, basterà dimostrare che
che è gruppo rispetto alla composizione, basterà dimostrare che
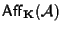 ne è sottogruppo, cioè dobbiamo dimostare che
ne è sottogruppo, cioè dobbiamo dimostare che
- se
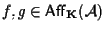 allora anche
allora anche 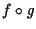 ci sta;
ci sta;
- se
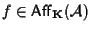 allora anche
allora anche
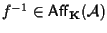 ;
;
-
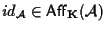 .
.
La dimostrazione di questi punti è identica nella sostanza a quella di esercizio 6 a cui rimandiamo.
Per dimostrare che
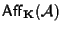 non è commutativo se
non è commutativo se
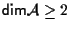 possiamo sfruttare il fatto che
possiamo sfruttare il fatto che
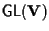 non è commutativo se
non è commutativo se
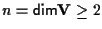 (infatti è isomorfo a
(infatti è isomorfo a
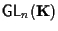 in cui l'operazione gruppale è la moltiplicazione di matrici e sappiamo immediatamente trovare controesempi di matrici invertibili
in cui l'operazione gruppale è la moltiplicazione di matrici e sappiamo immediatamente trovare controesempi di matrici invertibili 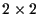 che non commutano.
che non commutano.
Ora, scelti
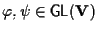 tali che
tali che
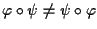 e
e
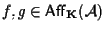 tali che
tali che
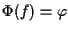 e
e
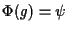 -scelta certamente possibile (vedi conclusioni successive a teorema 7)- affermiamo che
-scelta certamente possibile (vedi conclusioni successive a teorema 7)- affermiamo che
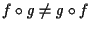 infatti
infatti
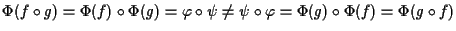 ove la prima uguaglianza è conseguenza della prima parte di questo esercizio -esattamente come in esercizio 6- (si noti per inciso che essa ci dice che
ove la prima uguaglianza è conseguenza della prima parte di questo esercizio -esattamente come in esercizio 6- (si noti per inciso che essa ci dice che 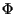 è un epimorfismo di gruppi).
è un epimorfismo di gruppi).
A questo punto concludiamo che 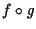 e
e 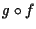 sono diversi in quanto hanno parti lineari diverse.
sono diversi in quanto hanno parti lineari diverse.

