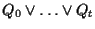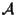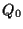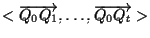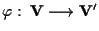10.3 Ancora una volta questo risultato scende dalle considerazioni della sezione "Sottospazi affini" che ci dicono che possiamo scrivere $Q_0\vee\ldots\vee Q_t$ come il sottospazio affine di $\mathcal{A}$ passante per $Q_0$ e di giacitura $<\overrightarrow{Q_0 Q_1},\ldots,\overrightarrow{Q_0 Q_t}>$ e poi basta imitare la dimostrazione di esercizio 10.1 (ogni volta si è applicato il fatto che se $\varphi:\;\mathbf{V}\longrightarrow\mathbf{V}'$ è un'applicazione lineare e $\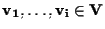mathbf{v_1},\ldots,\mathbf{v_i}\in\mathbf{V}$ allora $\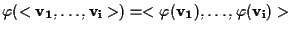varphi(<\mathbf{v_1},\ldots,\mathbf{v_i}>)=<\varphi(\mathbf{v_1} ),\ldots,\varphi(\mathbf{v_i})>$ a prescindere dal fatto che 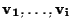$\mathbf{v_1},\ldots,\mathbf{v_i}$ siano indipendenti -come in esecizio 10.1 e 10.2- o meno).