6.
-
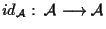 è isomorfismo affine, infatti
è isomorfismo affine, infatti
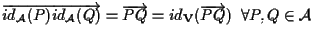 e certamente
e certamente
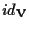 è un automorfismo di
è un automorfismo di
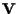 ;
si noti per inciso che abbiamo dimostrato che
;
si noti per inciso che abbiamo dimostrato che
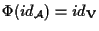 .
.
- Sia
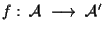 isomorfismo affine; affermiamo che
isomorfismo affine; affermiamo che
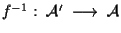 è isomorfismo affine e concludiamo (si noti che
è isomorfismo affine e concludiamo (si noti che 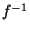 esiste perché
esiste perché 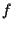 è biunivoca per ipotesi).
Siano
è biunivoca per ipotesi).
Siano
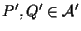 ,
poniamo
,
poniamo
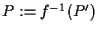 cioè
cioè 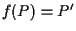 e
e
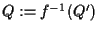 cioè
cioè 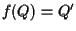 .
.
Poiché 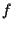 è applicazione affine potremo scrivere
è applicazione affine potremo scrivere
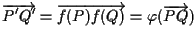 ove
ove
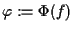 è biunivoca; in particolare potremo dire che
è biunivoca; in particolare potremo dire che
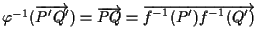 e concludiamo ricordando che, dall'algebra lineare, l'inverso di un isomorfismo di
e concludiamo ricordando che, dall'algebra lineare, l'inverso di un isomorfismo di
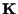 -spazi vettoriali è ancora tale. Si noti per inciso che abbiamo dimostrato che
-spazi vettoriali è ancora tale. Si noti per inciso che abbiamo dimostrato che
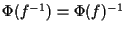 .
. - Siano
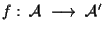 e
e
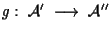 isomorfismi affini rispettivamente con parti lineari
isomorfismi affini rispettivamente con parti lineari
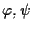 .
Affermiamo che
.
Affermiamo che
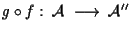 è isomorfismo affine; dati infatti
è isomorfismo affine; dati infatti
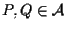 si ha che:
si ha che:
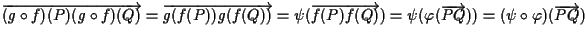 e siccome sappiamo dall'algebra lineare che
e siccome sappiamo dall'algebra lineare che
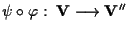 è isomorfismo di
è isomorfismo di
 -spazi vettoriali possiamo concludere. Si noti ancora che abbiamo dimostrato che
-spazi vettoriali possiamo concludere. Si noti ancora che abbiamo dimostrato che
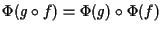 .
.

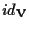 è un automorfismo di
è un automorfismo di
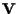 ;
si noti per inciso che abbiamo dimostrato che
;
si noti per inciso che abbiamo dimostrato che
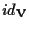 è un automorfismo di
è un automorfismo di
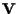 ;
si noti per inciso che abbiamo dimostrato che
;
si noti per inciso che abbiamo dimostrato che
