14.4
Per l'esercizio 14.1 sappiamo che
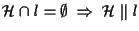 ;
viceversa sia
;
viceversa sia
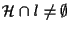 ;
dobbiamo provare che
;
dobbiamo provare che
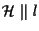 oppure che
oppure che
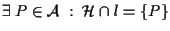 .
.
Se
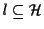 allora
allora
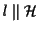 ,
supponiamo quindi
,
supponiamo quindi
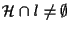 e
e
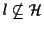 ,
allora in virtú di esercizio 9 della sezione "Sottospazi affini" possiamo affermare che
,
allora in virtú di esercizio 9 della sezione "Sottospazi affini" possiamo affermare che
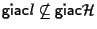 ;
di qui , da considerazioni di algebra lineare segue
;
di qui , da considerazioni di algebra lineare segue
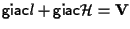 ;
allora da esercizio 16.2 della sezione "Sottospazi affini" segue che
;
allora da esercizio 16.2 della sezione "Sottospazi affini" segue che
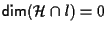 cioè
cioè
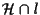 consiste di un solo punto.
consiste di un solo punto.

