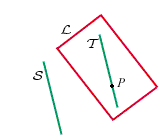
14.2
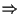 Per ipotesi abbiamo che
Per ipotesi abbiamo che
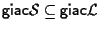 oppure
oppure
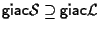 ;
d'altra parte abbiamo anche che
;
d'altra parte abbiamo anche che
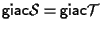 per cui
per cui
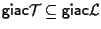 oppure
oppure
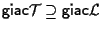 infine, ricordando che
infine, ricordando che
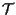 e
e
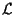 non sono disgiunti -ci sta certamente
non sono disgiunti -ci sta certamente 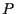 - otteniamo che
- otteniamo che
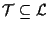 oppure
oppure
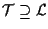 (si veda esercizio 9 della sezione "Sottospazi affini").
(si veda esercizio 9 della sezione "Sottospazi affini").
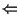 Viceversa supponiamo che
Viceversa supponiamo che
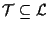 oppure
oppure
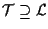 allora
allora
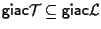 oppure
oppure
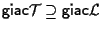 ;
ma essendo
;
ma essendo
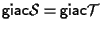 per cui otteniamo
per cui otteniamo
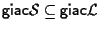 oppure
oppure
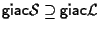 e cioè
e cioè
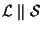 .
.