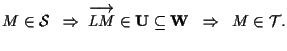9.
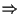 )
Se
)
Se
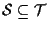 certamente
certamente
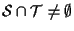 -ricordiamo che un sottospazio affine non è mai vuoto (vedi esercizio 2.3 della sezione corrente); dimostriamo che
-ricordiamo che un sottospazio affine non è mai vuoto (vedi esercizio 2.3 della sezione corrente); dimostriamo che
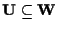 :
se
:
se
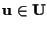
 (per la corrispondenza esaminata in osservazione 8 di questa sezione);
ma per ipotesi
(per la corrispondenza esaminata in osservazione 8 di questa sezione);
ma per ipotesi
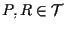 allora
allora
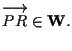 (esercizio 2.1 di questa sezione)
(esercizio 2.1 di questa sezione)
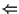 )
Sia
)
Sia
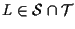 ;
allora potremo scrivere
;
allora potremo scrivere
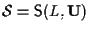 e
e
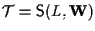 (si è utilizzato il contenuto di esercizio 2.4);
sia
(si è utilizzato il contenuto di esercizio 2.4);
sia
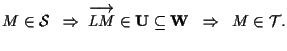

 (per la corrispondenza esaminata in osservazione 8 di questa sezione);
ma per ipotesi
(per la corrispondenza esaminata in osservazione 8 di questa sezione);
ma per ipotesi
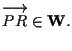 (esercizio 2.1 di questa sezione)
(esercizio 2.1 di questa sezione)