22.3
Per il primo punto si osservi che se
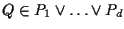 allora
allora
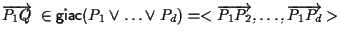 e quindi i vettori
e quindi i vettori
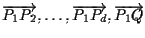 sono linearmente dipendenti per cui i punti
sono linearmente dipendenti per cui i punti
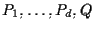 sono dipendenti.
sono dipendenti.
Viceversa se
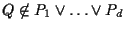 allora
allora
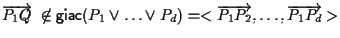 e quindi, da argomentazioni di algebra lineare, segue che i vettori
e quindi, da argomentazioni di algebra lineare, segue che i vettori
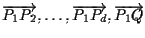 sono linearmente indipendenti per cui i punti
sono linearmente indipendenti per cui i punti
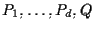 sono indipendenti.
sono indipendenti.
Per il secondo punto si imiti la dimostrazione di esercizio 22.1 sfruttando il risultato di algebra lineare in cui si afferma che, se
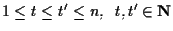 ed è assegnato un insieme di
ed è assegnato un insieme di 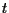 vettori linearmente indipendenti di
vettori linearmente indipendenti di
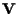 ,
allora è possibile trovare un secondo insieme di
,
allora è possibile trovare un secondo insieme di 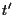 vettori linearmente indipendenti di
vettori linearmente indipendenti di
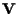 contenente il primo.
contenente il primo.

