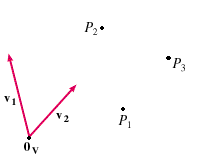
22.1
Sfruttiamo la caratterizzazione algebrica dell'indipendenza tra punti e il fatto che in uno spazio vettoriale 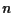 -dimensionale è sempre possibile trovare
-dimensionale è sempre possibile trovare 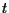 vettori indipendenti se
vettori indipendenti se
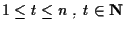 :
:
sia
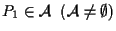 e siano
e siano
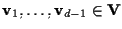 vettori linearmente indipendenti, ciò è lecito in quanto
vettori linearmente indipendenti, ciò è lecito in quanto
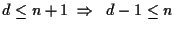 ;
siano
;
siano
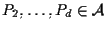 tali che
tali che
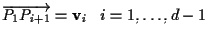 allora
allora
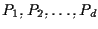 sono indipendenti.
sono indipendenti.