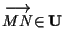2. ESERCIZI
2.1
Sia 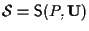 sottospazio affine di
sottospazio affine di
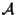 ;
siano
;
siano
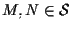 ,
dimostrare che
,
dimostrare che
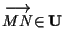
2.2
Sia
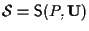 sottospazio affine di
sottospazio affine di
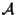 ;
dimostrare che
;
dimostrare che
in particolare
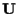 è univocamente determinato da
è univocamente determinato da
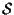 per cui si potrà parlare della giacitura di
per cui si potrà parlare della giacitura di
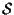 ;
essa verrà denotata col simbolo
;
essa verrà denotata col simbolo
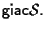
2.3
Sia
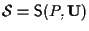 sottospazio affine di
sottospazio affine di
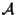 ;
dimostrare che
;
dimostrare che
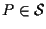 e ciò giustifica
la dicitura "
e ciò giustifica
la dicitura "
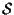 passante per
passante per 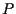 ".
".
2.4
Dato 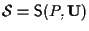 sottospazio affine di
sottospazio affine di 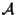 ,
abbiamo fatto vedere in esercizio 2.2 che
,
abbiamo fatto vedere in esercizio 2.2 che
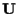 è univocamente determinato da
è univocamente determinato da 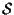 e in esercizio 2.3 che
e in esercizio 2.3 che
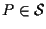 .
.
D'altra parte, come suggerito dalla dicitura "sottospazio passante per 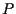 ",
ci possiamo aspettare, in generale, che
",
ci possiamo aspettare, in generale, che 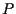 non sia univocamente determinato da
non sia univocamente determinato da
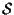 e che ogni altro punto giochi lo
stesso ruolo (perché "in generale"? in quale caso
e che ogni altro punto giochi lo
stesso ruolo (perché "in generale"? in quale caso 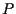 è univocamente determinato da
è univocamente determinato da
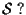 ).
).
A tal proposito si dimostri che vale
2.5
Sia
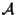 spazio affine e
spazio affine e
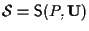 e
e
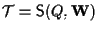 sottospazi affini di
sottospazi affini di
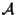 ,
vale:
,
vale: