7 Cominciamo col dimostrare la prima uguaglianza, cioè 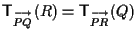$ \mathsf{T}_{\stackrel{\longrightarrow}{PQ}}(R)= \mathsf{T}_{\stackrel{\longrightarrow}{PR}}(Q)$ cioè
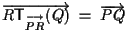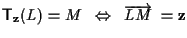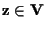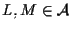$\overrightarrow{R\mathsf{T}_{\stackrel{\longrightarrow}{PR}}(Q)}\;=\; \overrightarrow{PQ}$ (si renda conto il lettore di ciò, ricordando che per definizione $\mathsf{T}_{\mathbf{z}}(L)=M\;\;\Leftrightarrow\;\;\overrightarrow{LM}\;=\mathbf{z}$ ove $ \mathbf{z} \in \mathbf{V}$ e $L,M \in \mathcal{A}$ )
Si ha dunque 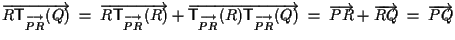$ \overrightarrow{R\mathsf{T}_{\stackrel{\longrightarrow}{PR}}(Q)}\;=\; \overrig... ...PR}}(Q)}\;=\; \overrightarrow{PR}+\overrightarrow{RQ}\;=\; \overrightarrow{PQ}$ e ciò conclude la dimostrazione della prima uguaglianza; si noti che 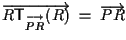$\overrightarrow{R\mathsf{T}_{\stackrel{\longrightarrow}{PR}}(R)}\;=\;\overrightarrow{PR}$ segue dalla definizione di traslazione, mentre 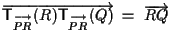$\overrightarrow{\mathsf{T}_{\stackrel{\longrightarrow}{PR}}(R)\mathsf{T}_{\stackrel{\longrightarrow}{PR}}(Q)}\;=\;\overrightarrow{RQ}$ segue da esercizio 4.
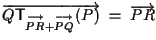
Rimane da dimostrare la seconda uguaglianza, cioè $\overrightarrow{Q \mathsf{T}_{\stackrel{\longrightarrow}{PR}+\stackrel{\longrightarrow}{PQ}}(P)}\;=\;\overrightarrow{PR}$
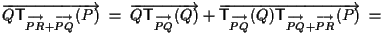
Si ha $ \overrightarrow{Q \mathsf{T}_{\stackrel{\longrightarrow}{PR}+\stackrel{\longri... ...athsf{T}_{\stackrel{\longrightarrow}{PQ}+\stackrel{\longrightarrow}{PR}}(P)}\;=$
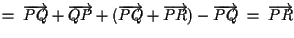
$=\;\overrightarrow{PQ}+\overrightarrow{QP}+( \overrightarrow{PQ}+\overrightarrow{PR})-\overrightarrow{PQ}\;=\; \overrightarrow{PR}$
e ciò conclude la dimostrazione della seconda uguaglianza; si noti che 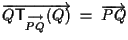$\overrightarrow{Q\mathsf{T}_{\stackrel{\longrightarrow}{PQ}}(Q)}\;=\;\overrightarrow{PQ}$ per definizione di traslazione e 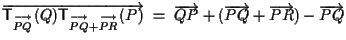$\overrightarrow{\mathsf{T}_{\stackrel{\longrightarrow}{PQ}}(Q)\mathsf{T}_{\stac... ...verrightarrow{QP}+(\overrightarrow{PQ}+\overrightarrow{PR})-\overrightarrow{PQ}$ da esercizio 6.