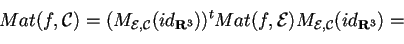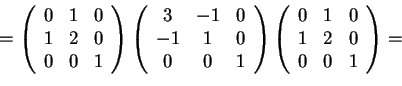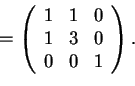- a)
- Dobbiamo diagonalizzare la forma
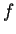 :
:
prendiamo un vettore
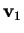 non isotropo, ad esempio
non isotropo, ad esempio
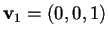 e calcoliamo il suo sottospazio ortogonale:
e calcoliamo il suo sottospazio ortogonale:
da cui otteniamo
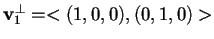 .
Scegliamo ora uno dei due vettori che generano il sottospazio ortogonale, ad esempio
.
Scegliamo ora uno dei due vettori che generano il sottospazio ortogonale, ad esempio
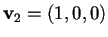 ,
e procediamo in modo analogo:
,
e procediamo in modo analogo:
Risolvendo il seguente sistema, otteniamo il terzo vettore della base diagonalizzante per 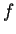 :
:
per cui
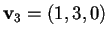 .
Trovata la base diagonalizzante
.
Trovata la base diagonalizzante
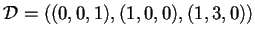 ,
determiniamo la matrice diagonale congruente a
,
determiniamo la matrice diagonale congruente a
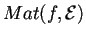 :
:
La forma 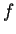 ha quindi tre autovalori positivi, perciò la sua segnatura è (3,0); questo implica anche che non può esistere una base
ha quindi tre autovalori positivi, perciò la sua segnatura è (3,0); questo implica anche che non può esistere una base
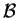 richiesta come sopra perché, per qualsialsi base
richiesta come sopra perché, per qualsialsi base
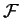 di
di
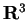 ,
,
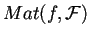 appartiene alla classe di congruenza di
appartiene alla classe di congruenza di 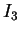 ,
essendo
,
essendo 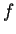 un prodotto scalare.
un prodotto scalare.
- b)
- Risolviamo questo punto con un semplice prodotto di matrici:



:
non isotropo, ad esempio
e calcoliamo il suo sottospazio ortogonale:
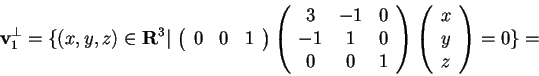
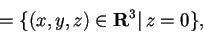
. Scegliamo ora uno dei due vettori che generano il sottospazio ortogonale, ad esempio
, e procediamo in modo analogo:
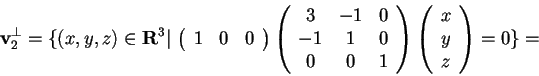
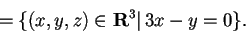
:
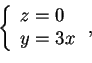
. Trovata la base diagonalizzante
, determiniamo la matrice diagonale congruente a
:
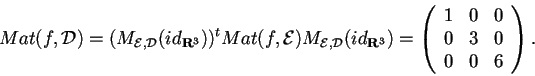
ha quindi tre autovalori positivi, perciò la sua segnatura è (3,0); questo implica anche che non può esistere una base
richiesta come sopra perché, per qualsialsi base
di
,
appartiene alla classe di congruenza di
, essendo
un prodotto scalare.