Soluzione3

Soluzione

a)
Poiché

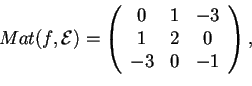
$\begin{displaymath}Mat(f,\mathcal{E})=\begin{array}({ccc}) 0 & 1 & -3\\ 1 & 2 & 0\\ -3 & 0 & -1 \end{array}, \end{displaymath}$

per trovare la matrice richiesta, basta fare un semplice calcolo matriciale:

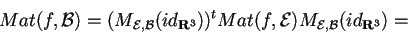
$\begin{displaymath}Mat(f,\mathcal{B})=(M_{\mathcal{E,B}}(id_{\mathbf{R}^3}))^{t}Mat(f,\mathcal{E})M_{\mathcal{E,B}}(id_{\mathbf{R}^3})= \end{displaymath}$

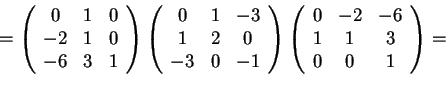
$\begin{displaymath}=\begin{array}({ccc}) 0 & 1 & 0\\ -2 & 1 & 0\\ -6 & 3 & ... ...{ccc}) 0 & -2 & -6\\ 1 & 1 & 3\\ 0 & 0 & 1 \end{array}= \end{displaymath}$

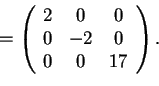
$\begin{displaymath}=\begin{array}({ccc}) 2 & 0 & 0\\ 0 & -2 & 0\\ 0 & 0 & 17 \end{array}. \end{displaymath}$

La base $\mathcal{B}$ è diagonalizzante per , quindi possiamo subito affermare che la segnatura della forme bilineare simmetrica è (2,1).
b)
Per verificare che il vettore $\mathbf{v}$ è non isotropo, dobbiamo provare che $f(\mathbf{v},\mathbf{v})\neq 0$ , infatti:

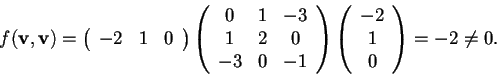
$\begin{displaymath}f(\mathbf{v},\mathbf{v})=\begin{array}({ccc}) -2 & 1 & 0 \e... ...y} \begin{array}({c}) -2\\ 1\\ 0 \end{array}=-2\neq 0. \end{displaymath}$

Ora determiniamo $\mathbf{v}^{\perp}$ :

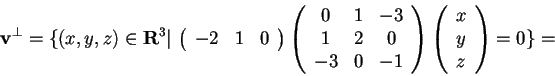
$\begin{displaymath}\mathbf{v}^{\perp}=\{ (x,y,z)\in\mathbf{R}^3 \vert \,\begin{a... ...{array} \begin{array}({c}) x\\ y\\ z \end{array}=0 \}= \end{displaymath}$

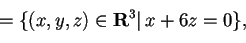
$\begin{displaymath}=\{ (x,y,z)\in\mathbf{R}^3 \vert \, x+6z=0 \}, \end{displaymath}$

da cui otteniamo che $\mathbf{v}^{\perp}=<(-6,0,1),(0,1,0)>$ .