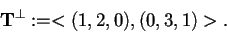- a)
- Affinché due matrici siano congruenti come matrici reali, devono avere la stessa segnatura; controlliamo in prima istanza che abbiano rango uguale:
quindi, essendo 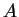 una matrice non degenere, ha rango massimo, cioè
una matrice non degenere, ha rango massimo, cioè 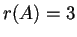 (quindi anche
(quindi anche 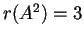 poiché
poiché
 ).
).
Calcoliamo ora 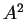 :
:
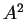 è già diagonalizzata e possiamo vedere subito che ha 3 autovalori positivi, quindi la sua segnatura è (3,0).
Dobbiamo trovare una base diagonalizzante per
è già diagonalizzata e possiamo vedere subito che ha 3 autovalori positivi, quindi la sua segnatura è (3,0).
Dobbiamo trovare una base diagonalizzante per 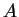 :
:
prendiamo un vettore non isotropo, ad esempio
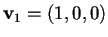 e determiniamo
e determiniamo
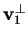 :
:
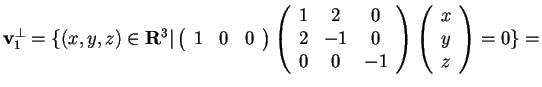
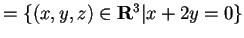
,
da cui otteniamo che
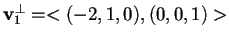 .
Scegliamo
.
Scegliamo
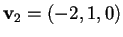 ,
allora avremo che
,
allora avremo che
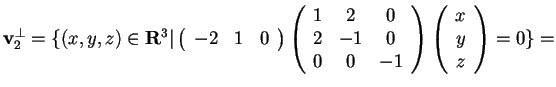
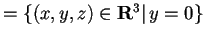
;
quindi otteniamo il terzo vettore della base risolvendo il sistema
che risulta essere
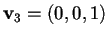 .
Quindi
.
Quindi
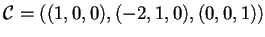 è una base diagonalizzante per la matrice
è una base diagonalizzante per la matrice 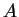 ,
perciò otterremo una matrice diagonale
,
perciò otterremo una matrice diagonale 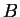 ,
,
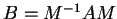 ,
ove
,
ove 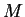 è la matrice del cambiamento di base da
è la matrice del cambiamento di base da 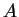 a
a 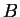 :
:
La segnatura di 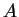 è (1,2) perché ha un autovalore positivo e due negativi, quindi le due matrici non sono congruenti come matrici reali.
L'unica condizione affinché due matrici siano congruenti come matrici complesse è che abbiano lo stesso rango, quindi le matrici complesse
è (1,2) perché ha un autovalore positivo e due negativi, quindi le due matrici non sono congruenti come matrici reali.
L'unica condizione affinché due matrici siano congruenti come matrici complesse è che abbiano lo stesso rango, quindi le matrici complesse 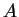 e
e 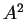 sono congruenti.
sono congruenti.
- b)
- Abbiamo già trovato che la segnatura di
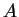 è (1,2), perciò la forma canonica per
è (1,2), perciò la forma canonica per 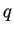 è
è
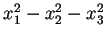 .
Un vettore
.
Un vettore
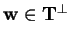 se
se
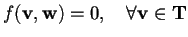 .
Quindi il sottospazio vettoriale
.
Quindi il sottospazio vettoriale
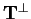 è equivalente al sottospazio delle soluzioni del sistema omogeneo
è equivalente al sottospazio delle soluzioni del sistema omogeneo
ed è quindi determinato dall'equazione 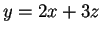 ;
perciò
;
perciò




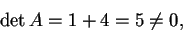
una matrice non degenere, ha rango massimo, cioè
(quindi anche
poiché
).
:
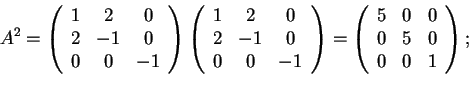
è già diagonalizzata e possiamo vedere subito che ha 3 autovalori positivi, quindi la sua segnatura è (3,0). Dobbiamo trovare una base diagonalizzante per
:
e determiniamo
:
da cui otteniamo che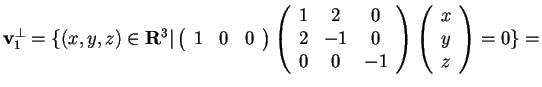
,
. Scegliamo
, allora avremo che
quindi otteniamo il terzo vettore della base risolvendo il sistema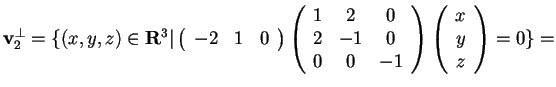
;
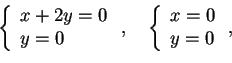
. Quindi
è una base diagonalizzante per la matrice
, perciò otterremo una matrice diagonale
,
, ove
è la matrice del cambiamento di base da
a
:
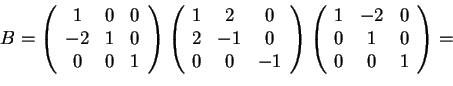
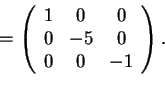
è (1,2) perché ha un autovalore positivo e due negativi, quindi le due matrici non sono congruenti come matrici reali. L'unica condizione affinché due matrici siano congruenti come matrici complesse è che abbiano lo stesso rango, quindi le matrici complesse
e
sono congruenti.
è (1,2), perciò la forma canonica per
è
. Un vettore
se
. Quindi il sottospazio vettoriale
è equivalente al sottospazio delle soluzioni del sistema omogeneo
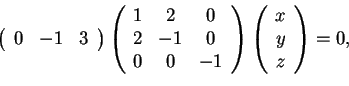
; perciò