

- a)
- Dobbiamo diagonalizzare
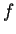 :
:
prendiamo un vettore non isotropo, ad esempio
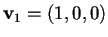 ,
e calcoliamo il suo sottospazio ortogonale:
,
e calcoliamo il suo sottospazio ortogonale:
da cui si ha:
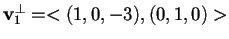 .
Scegliamo come secondo vettore
.
Scegliamo come secondo vettore
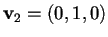 e procediamo in modo analogo:
e procediamo in modo analogo:
Il terzo vettore della base diagonalizzante è dato dall'intersezione dei sottospazi ortogonali ai primi due vettori:
perciò otteniamo che
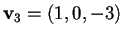 .
Trovata la base diagonale
.
Trovata la base diagonale
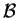 cercata, diagonalizziamo
cercata, diagonalizziamo 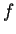 :
:
.
La segnatura di 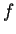 è (2,1) e la sua forma canonica diventa:
è (2,1) e la sua forma canonica diventa:
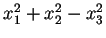 .
.
Inoltre 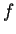 non è un prodotto scalare, ma una forma indefinita.
non è un prodotto scalare, ma una forma indefinita.
- b)
- Troviamo i vettori che generano
 :
:
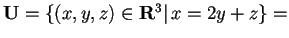
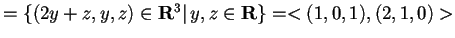
.
Il sottospazio vettoriale
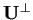 è dato dall'intersezione dei sottospazi ortogonali ai vettori che generano
è dato dall'intersezione dei sottospazi ortogonali ai vettori che generano
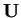 ,
quindi
,
quindi
perciò dallo spazio delle soluzioni del sistema
Quindi una base per il sottospazio vettoriale
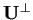 di dimensione 1 è
di dimensione 1 è
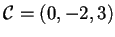 .
.



:
, e calcoliamo il suo sottospazio ortogonale:
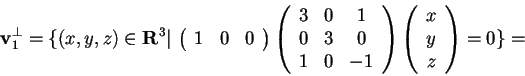
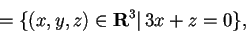
. Scegliamo come secondo vettore
e procediamo in modo analogo:

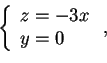
. Trovata la base diagonale
cercata, diagonalizziamo
:
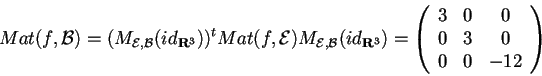
è (2,1) e la sua forma canonica diventa:
.
non è un prodotto scalare, ma una forma indefinita.
:
Il sottospazio vettoriale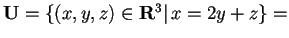
.
è dato dall'intersezione dei sottospazi ortogonali ai vettori che generano
, quindi
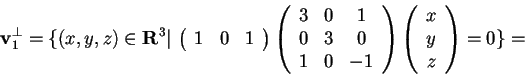
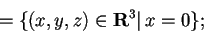
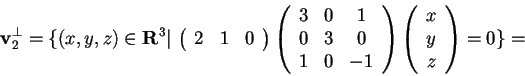
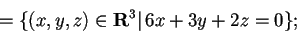
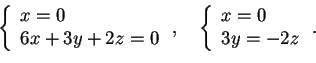
di dimensione 1 è
.

