Regola di de l'Hôpital

Nell'analisi matematica la regola di de l'Hôpital è un procedimento che permette di calcolare vari limiti di quozienti di funzioni reali di variabile reale che convergono a forme indeterminate delle forme 0/0 e $\infty$ / $\infty$ con l'aiuto della derivata del numeratore e della derivata del denominatore. La regola si può estendere per cercare di calcolare limiti di funzioni appartenenti ad altre forme indeterminate.

Il teorema

************

Siano f, g : [a,b] à $\Bbb{R}$ due funzioni reali di variabile reale continue in [a,b] e derivabili in (a,b), con - $\infty$ ≤ a < b ≤ + $\infty$ ; siano g(x) e g’(x) diverse da 0 in ogni punto di tale intervallo, tranne al più in c∈ (a,b). Sia inoltre

$\left( f(x) \wedge g(x) \right) \underset{x \rightarrow c}{\longrightarrow} 0$

oppure

$\left( f(x) \wedge g(x) \right) \underset{x \rightarrow c}{\longrightarrow} \pm\infty$

ed esista

$L \in \mathbb{\bar{R}} = \lim_{x \to c}{\frac{f'(x)}{g'(x)}}$ .

Allora

$\lim_{x \to c}{\frac{f(x)}{g(x)}} = L$ .

Perciò, se si cerca un limite di un quoziente il cui numeratore e denominatore convergono entrambi a zero, oppure divergono entrambi ad infinito, può essere utile cercare di calcolare il quoziente delle derivate del numeratore e del denominatore. Se esiste il limite L di questo nuovo quoziente, allora esisterà anche il limite del quoziente originale e coinciderà con L. Se invece il nuovo quoziente a sua volta appartiene ad una forma indeterminata, si può ripetere l'operazione, cioè cercare di calcolare il limite del quoziente delle derivate seconde e così via.

L'incapacità di determinare il limite del quoziente delle derivate comunque non implica la non esistenza del limite del quoziente originale.

Dimostrazione

*****************

La dimostrazione usuale fa uso del teorema di Cauchy ed è soggetta a variazioni a seconda che e siano finiti o infiniti, che f e g convergano a zero o ad infinito, e che i limiti in considerazione siano destri, sinistri o bilateri. Tutte queste varianti seguono le due versioni principali qui sotto esposte, con opportune precisazioni, ma senza bisogno di introdurre nuovi ragionamenti. Inoltre è opportuno ricordare che ogni forma di indeterminazione del tipo "zero su zero" o "infinito su infinito" è riconducibile ciascuna all'altra; pertanto è sufficiente dimostrarne una delle due per ottenere automaticamente anche l'altra.

Zero su zero

***************

Si considerino ed reali e f(x) e g(x) funzioni convergenti a zero per $x\to c$ .

Pertanto è possibile supporre che sia f(c)= 0 e g(c)=0.

Questo implica la possibilità di considerare sia f che g continue in , senza per questo modificarne il limite (infatti, per definizione, il limite non dipende dalla valutazione nel punto ).

Poiché esiste lim_x_à_cf’(x)/g’(x), esiste un intervallo (c- δ, c+ δ) tale che per ogni nell'intervallo, eccetto al più stesso, sia f’(x) che g’(x) esistono e g’(x) ≠ 0.

Se x∈ (c, c+ δ), si possono applicare sia il teorema del valor medio che il teorema di Cauchy sull'intervallo [c,x] (lo stesso vale, con argomentazioni simili, nell'intervallo (c- δ, c)). Il teorema del valor medio implica che su tale intervallo sia g(x) ≠ 0 (altrimenti esisterebbe y ∈ (c, x) con g’(y)=0). Il teorema di Cauchy asserisce che esiste un punto $\xi_x$ in (c, x) tale che

$\frac{f(x)}{g(x)} = \frac{f'(\xi_x)}{g'(\xi_x)}.$

Se x tende a c, allora $\xi_x$ tende a c. Poiché lim_x_à_cf’(x)/g’(x) esiste, segue che

$\lim_{x\to c}\frac{f(x)}{g(x)} = \lim_{x\to c}\frac{f'(\xi_x)}{g'(\xi_x)} = \lim_{x\to c}\frac{f'(x)}{g'(x)}.$

Infinito su infinito

************************

Si consideri finito, e f e g convergenti a + $\infty$ per x à + $\infty$ .

Per ogni $\varepsilon >0$ , esiste tale che

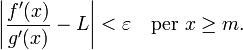
$\left|\frac{f'(x)}{g'(x)} - L\right| < \varepsilon \quad \text{per } x\geq m.$

Il teorema del valor medio implica che se , allora g(x) ≠ g(m) (altrimenti esisterebbe y∈(m,x) con g’(y) = 0). Il teorema di Cauchy applicato all'intervallo [m,x] garantisce che

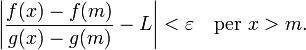
$\left|\frac{f(x)-f(m)}{g(x)-g(m)} - L\right| < \varepsilon \quad \text{per } x>m.$

Poiché f diverge a + $\infty$ , se x è sufficientemente grande, allora f(x) ≠ f(m). Dunque si potrà scrivere

$\frac{f(x)}{g(x)} = \frac{f(x)-f(m)}{g(x)-g(m)} \cdot \frac{f(x)}{f(x)-f(m)} \cdot \frac{g(x)-g(m)}{g(x)}.$

Si consideri,

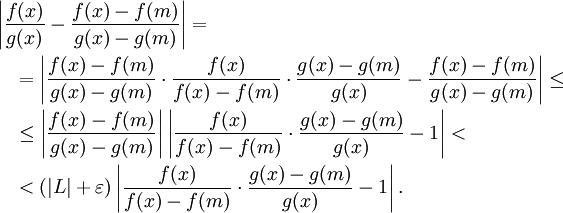
$\begin{align} &\left|\frac{f(x)}{g(x)}- \frac{f(x)-f(m)}{g(x)-g(m)}\right|=\\ &\quad = \left|\frac{f(x)-f(m)}{g(x)-g(m)} \cdot \frac{f(x)}{f(x)-f(m)} \cdot \frac{g(x)-g(m)}{g(x)} - \frac{f(x)-f(m)}{g(x)-g(m)}\right| \leq\\ & \quad \leq \left|\frac{f(x)-f(m)}{g(x)-g(m)}\right| \left|\frac{f(x)}{f(x)-f(m)} \cdot \frac{g(x)-g(m)}{g(x)} - 1\right| <\\ & \quad < (|L|+\varepsilon)\left|\frac{f(x)}{f(x)-f(m)} \cdot \frac{g(x)-g(m)}{g(x)} - 1\right|. \end{align}$

Per sufficientemente grande, questo è meno di qualunque $\varepsilon$ e dunque

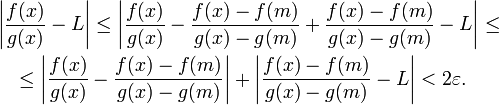
$\begin{align}&\left|\frac{f(x)}{g(x)}-L\right|\leq\left|\frac{f(x)}{g(x)} - \frac{f(x)-f(m)}{g(x)-g(m)}+ \frac{f(x)-f(m)}{g(x)-g(m)}-L\right|\leq\\ &\quad \leq \left|\frac{f(x)}{g(x)} - \frac{f(x)-f(m)}{g(x)-g(m)}\right|+ \left|\frac{f(x)-f(m)}{g(x)-g(m)}-L\right|< 2\varepsilon.\end{align}$

Il che implica che:

$\lim_{x\to +\infty}\frac{f(x)}{g(x)} = \lim_{x\to +\infty}\frac{f'(x)}{g'(x)}=L.$

Indice