Estensione al caso infinito 

La definizione di limite viene normalmente estesa per considerare anche i casi in cui x0 e/o  l  sono infiniti.

La funzione f  ha limite infinito in un punto finito x0 se

per ogni numero reale N > 0 esiste un altro numero reale δ > 0 tale che f(x) > N per ogni x in  X  con 0 < |x- x0| < δ.

In questo caso si scrive

\lim_{x \to x_0}f(x) = +\infty.

Analogamente si definisce il limite -\infty sostituendo f(x) > N con f(x) < - N .

Per definire il limite per  x0 à +\infty, è ancora necessario che x0 sia "punto di accumulazione" per il dominio  X : questo si traduce nella richiesta che  X  contenga valori arbitrariamente grandi, cioè che il suo estremo superiore sia infinito.

In questo caso, un numero finito  l  è limite di f  per x à +\infty se:

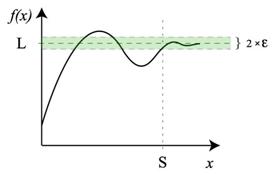
Per ogni numero reale ε > 0 esiste un altro numero reale S > 0 tale che

| f(x) - l |  < ε per ogni  x  in  X  con x > S.

In questo caso si scrive

\lim_{x\to+\infty}f(x) = l.

 

Analogamente si definisce il limite per x à - \infty , sostituendo x > S con x < - S.

La funzione f  ha limite +\infty per x à +\infty per ogni numero reale N > 0 esiste un altro numero reale S > 0 tale che

f(x) > N per ogni  x  in  X  con x > S .

In questo caso si scrive

\lim_{x\to+\infty}f(x) = +\infty.

Si definiscono analogamente i casi in cui x0 e/o  l  tendono al -\infty.

 

Terminologia

Se una funzione ha limite zero in x0, questa si dice infinitesima in x0. D'altro canto, se ha limite \pm\infty  è detta divergente.

Se x0 è contenuto nel dominio  X  di f , e se vale

\lim_{x\to x_0} f(x) = f(x_0)

allora la funzione è continua in x0. La nozione di continuità è molto importante in matematica: intuitivamente, una funzione continua in x0 ha il grafico che "non fa salti" intorno al punto, ma può essere disegnato manualmente senza staccare mai la penna dal foglio. Altrimenti, la funzione ha in x0 un punto di discontinuità.