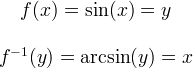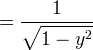Esempio

Le funzioni che meglio si prestano per applicare la regola di dervazione dell'inversa sono quelle trigonometriche.

Le funzioni trigonometriche in genere non sono iniettive, per poter lavorare con le loro funzioni inverse dobbiamo restringere i domini in modo adeguato.

(1) Arcoseno

Ricordando la formula per la derivata dell'inversa calcoliamo per prima cosa:

Ora, siccome vogliamo che la derivata dipenda da , sostituiamo

Come vediamo nell'immagine a fianco l'ultima ugualianza è spiegata dal fatto che se abbiamo un angolo di cui conosciamo il suo seno , il coseno di quell'angolo vale allora la lunghezza del cateto base che troviamo semplicemente con il teorema di Pitagora cioè .

In conclusione se vogliamo scrivere la derivata della funzione arcoseno in notazione normale con la variabile otteniamo:

(2) Arcocoseno

(3) Arcotangente