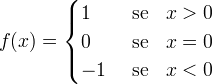Esempio

(1) Funzione discontinua quindi non derivabile

è discontinua in 0 e si noti come nel punto di ascissa 0 il grafico fa un salto è quindi intuitivo pensare che non si può tracciare la tangente al grafico in quel punto.

Per la precisione:

perciò non può esistere il limite del rapporto incrementale in 0 e quindi

non è derivabile in 0.

(2) Funzione continua ma non derivabile

Il valore assoluto è una funzione continua, ma come abbiamo visto in un esempio precedente non è derivabile.

Osserviamo che in 0 il grafico ha un punto angoloso dove non è possibile definire la tangente perchè dalla parte sinistra sarebbe la bisettrice del 2° e 4° quadrante, mentre da destra sarebbe la bisettrice del 1° e 3°.

(3) Funzione derivabile quindi continua

L'esponenziale è derivabile su tutto , quindi è anche continua. Notiamo che il grafico della funzione non ha spigoli.

In parole povere se una funzione è derivabile possiamo pensare al suo grafico come una curva "liscia" o regolare.