Significato geometrico
Consideriamo il grafico 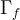 di una funzione reale di variabile reale di una funzione reale di variabile reale 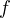 . .
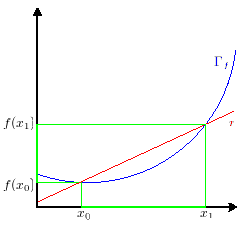 |
Se fissiamo 2 punti del piano
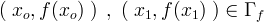
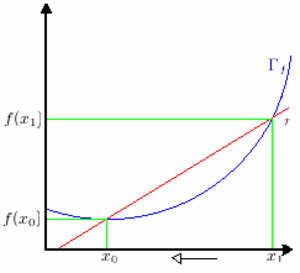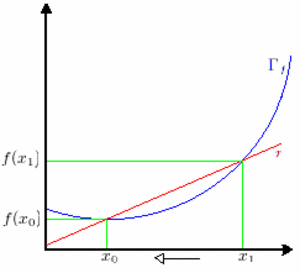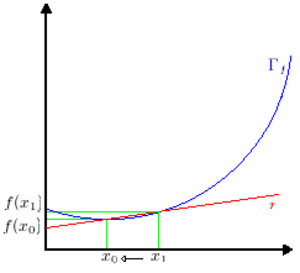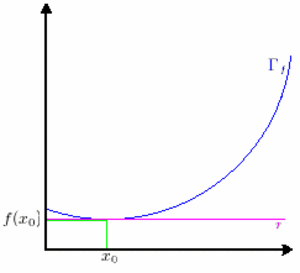
tracciando la retta passante per questi 2 punti otteniamo una SECANTE al grafico.
La secante r ha equazione :
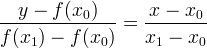
|
In forma esplicita
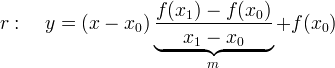
Notiamo che il coefficente angolare m della secante è il rapporto incrementale di 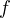 di punto iniziale di punto iniziale 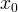 . .
Come mostrato nell'animazione a fianco se facciamo tendere 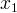 a a 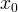 otteniamo una serie di secanti che al limite intersecano il grafico solo in otteniamo una serie di secanti che al limite intersecano il grafico solo in 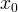 . .
Quindi abbiamo ottenuto una TANGENTE al grafico in 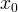 . .
Il coefficiente angolare della tangente risulta:

|
 |
In conclusione abbiamo dimostrato che la derivata di 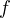 in in 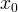 cioè cioè 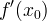 rappresenta il coefficiente angolare, ossia la pendenza della retta tangente in rappresenta il coefficiente angolare, ossia la pendenza della retta tangente in 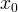 al grafico di al grafico di 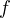 . .
|