Osservazione 1  

 Vertice $V$ e fuoco $F$ sono entrambi sull'asse di simmetria. Tale asse è ortogonale alla direttrice $d$.

Osservazione 2  

 Dalla definizione di fuoco e di direttrice segue che $\vert p\vert$ è la distanza tra fuoco e direttrice.

 

Osservazione 3 (Parabola con asse verticale)  

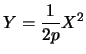 L'equazione $\displaystyle Y=\frac{1}{2p}X^2$ è una parabola con asse di simmetria l'asse $Y$. La verifica è immediata, basta infatti prendere $\mathcal{C}$ di equazione $y^2=2px$ e fare un cambiamento di coordinate del tipo

\begin{displaymath} \left\{ \begin{array}{c} x=Y\\ y=X. \end{array} \right. \end{displaymath} (1)
Ovviamente nel nuovo sistema di riferimento il vertice sarà sempre
$V=(0,0)$, il fuoco sarà $\displaystyle F=(0,\frac{p}{2})$, la direttrice sarà $\displaystyle Y=-\frac{p}{2}$.
Figura: L'asse y è l'asse di simmetria.
\includegraphics[width=9cm,height=7.5cm]{p-verticale}