Equazione polare della Parabola.
Consideriamo una parabola di fuoco 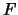 , direttrice
, direttrice 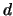 ed un punto
ed un punto
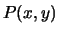 sulla parabola.
sulla parabola.
Fissiamo ora un sistema di riferimento 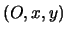 ortonormale in modo che:
ortonormale in modo che:
- 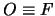 , cioè l'origine degli assi coincida con il fuoco.
, cioè l'origine degli assi coincida con il fuoco.
- l'asse 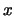 sia orientato da
sia orientato da 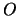 verso
verso 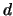 .
.
Adesso prendiamo 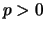 la distanza tra l'origine
la distanza tra l'origine 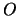 e il punto di
intersezione tra la direttrice d con l'asse
e il punto di
intersezione tra la direttrice d con l'asse 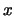 ,
, 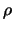 la
lunghezza del vettore
la
lunghezza del vettore
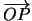 ,
, 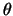 l'angolo che
l'angolo che
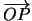 forma con l'asse
forma con l'asse 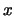 . Per costruzione quindi
. Per costruzione quindi
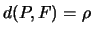 e
e
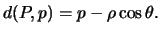 Se prima sostituiamo a
Se prima sostituiamo a
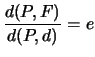 ed esplicitiamo poi
ed esplicitiamo poi
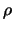 si ottiene:
Poichè
si ottiene:
Poichè 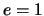 , allora
, allora
Tale equazione si chiama equazione polare
della
parabola.
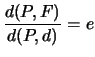 ed esplicitiamo poi
ed esplicitiamo poi