Dimostrazione
Per dimostrare tale risultato consideriamo la figura seguente e
supponiamo che in F vi sia una sorgente luminosa di cui uno dei
raggi sia incidente in P. Prendiamo ora la retta passante per 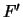 e P. Supponiamo ora (lo dimostreremo poi) che la bisettrice
dell'angolo
e P. Supponiamo ora (lo dimostreremo poi) che la bisettrice
dell'angolo
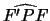 coincide con la retta tangente
all'iperbole nel punto
coincide con la retta tangente
all'iperbole nel punto 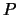 . Sia ora B un punto qualsiasi della
bisettrice dell'angolo
. Sia ora B un punto qualsiasi della
bisettrice dell'angolo
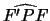 e
e 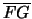 sia
perpendicolare a
sia
perpendicolare a 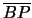 . Prendiamo ora, la retta passante
per P e perpendicolare a
. Prendiamo ora, la retta passante
per P e perpendicolare a 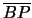 , N punto interno al ramo
di iperbole sulla retta per P . Segue che
, N punto interno al ramo
di iperbole sulla retta per P . Segue che 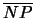 e
e
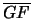 sono rette parallele ed il triangolo GPF è
isoscele, di conseguenza, gli angoli in
sono rette parallele ed il triangolo GPF è
isoscele, di conseguenza, gli angoli in 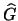 ed in
ed in
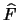 di tale triangolo sono uguali. D'altronde l'angolo
di tale triangolo sono uguali. D'altronde l'angolo
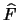 è uguale all'angolo di incidenza
è uguale all'angolo di incidenza 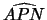 essendo questi angoli alterni interni, e l'angolo
essendo questi angoli alterni interni, e l'angolo 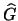 è
uguale all'angolo in
è
uguale all'angolo in 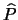 , essendo questi angoli
corrispondenti. Pertanto l'angolo di incidenza
, essendo questi angoli
corrispondenti. Pertanto l'angolo di incidenza 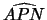 è
uguale all'angolo
è
uguale all'angolo 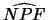 . Da questo risultato e dalla
legge di riflessione della luce concludiamo che quest'ultimo
angolo è proprio l'angolo di riflessione. Abbiamo quindi
dimostrato che il raggio riflesso passa per una traiettoria
uscente dall'altro fuoco.
. Da questo risultato e dalla
legge di riflessione della luce concludiamo che quest'ultimo
angolo è proprio l'angolo di riflessione. Abbiamo quindi
dimostrato che il raggio riflesso passa per una traiettoria
uscente dall'altro fuoco.
Figura:
La legge di riflessione dice che gli angoli 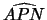 e l'angolo
e l'angolo 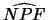 sono uguali
sono uguali
|
|
Per dimostrare che la bisettrice 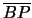 è allo stesso
tempo la tangente all'iperbole nel punto P basta vedere che, con
riferimento sempre alla figura seguente,
è allo stesso
tempo la tangente all'iperbole nel punto P basta vedere che, con
riferimento sempre alla figura seguente,
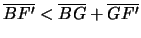 , quindi
, quindi
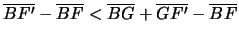 ,
poichè
,
poichè
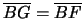 (GBF triangolo isoscele),
allora
(GBF triangolo isoscele),
allora
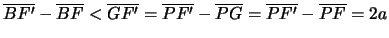 .
Questo mi dice che il punto B è esterno al ramo di iperbole
passante per P; cioè la bisettrice
.
Questo mi dice che il punto B è esterno al ramo di iperbole
passante per P; cioè la bisettrice 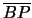 incontra
l'iperbole soltanto nel punto P che è appunto la retta tangente
all'iperbole nel punto P.
incontra
l'iperbole soltanto nel punto P che è appunto la retta tangente
all'iperbole nel punto P.
![\includegraphics[width=9cm,height=7.5cm]{i-geom_ott}](img18.png)