Regione in cui si trova la curva.
Intersechiamo l'iperbole con le rette parallele agli assi
coordinati e con quelle passanti per l'origine:
- sia
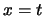 una retta parallela all'asse
una retta parallela all'asse 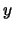
sostituendo tale valore a 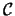 si ha:
si ha:
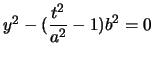 con
con
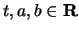 . Al variare di t avremo soluzioni diverse.
Infatti:
. Al variare di t avremo soluzioni diverse.
Infatti:
- se
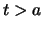 opp.
opp. 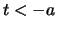 , la retta
, la retta 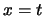 interseca la conica in due punti distinti;
interseca la conica in due punti distinti;
- se
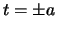 , interseca
, interseca 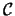 in due punti coincidenti;
in due punti coincidenti;
- se
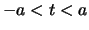 , interseca
, interseca 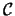 in due punti complessi e coniugati.
Quindi non ci sono intersezioni nel piano euclideo.
in due punti complessi e coniugati.
Quindi non ci sono intersezioni nel piano euclideo.
- sia
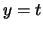 una retta parallela all'asse
una retta parallela all'asse 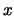
sostituendo in 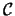 si ha:
si ha:
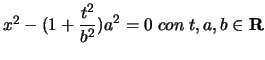 . Questo ci dice che qualunque sia
. Questo ci dice che qualunque sia 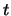 si hanno
sempre radici reali e la retta
si hanno
sempre radici reali e la retta 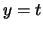 interseca l'iperbole in due
punti reali e distinti.
interseca l'iperbole in due
punti reali e distinti.
- sia
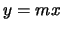 una retta per l'origine
una retta per l'origine
abbiamo sempre sostituendo in 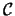 :
:
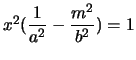 quindi:
quindi:
- se
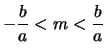 ,
,
la retta 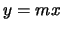 taglia
taglia 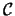 in due punti distinti
in due punti distinti
- se
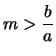 oppure
oppure
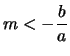 ,
,
interseca 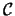 in due punti complessi e coniugati,
quindi non la interseca nel piano euclideo.
in due punti complessi e coniugati,
quindi non la interseca nel piano euclideo.
- se
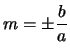 .
.
nessuna intersezione, nemmeno complessa, (vedremo più avanti che
queste rette sono asintoti)
Figura:
La regione delimitata dalle rette è
la regione in cui si svolge il grafico.
|
|
I punti
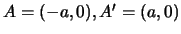 sono i punti di intersezione
di
sono i punti di intersezione
di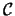 con l'asse
con l'asse 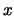 . Tali punti si chiamano
vertici dell'iperbole. La retta
. Tali punti si chiamano
vertici dell'iperbole. La retta 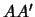 (che è uno degli
assi di simmetria) si chiama asse trasverso (o
asse focale o asse secante)dell'iperbole .
(che è uno degli
assi di simmetria) si chiama asse trasverso (o
asse focale o asse secante)dell'iperbole .
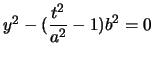 con
con
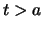 opp.
opp. 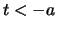 , la retta
, la retta 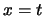 interseca la conica in due punti distinti;
interseca la conica in due punti distinti;
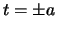 , interseca
, interseca 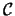 in due punti coincidenti;
in due punti coincidenti;
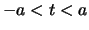 , interseca
, interseca 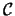 in due punti complessi e coniugati.
Quindi non ci sono intersezioni nel piano euclideo.
in due punti complessi e coniugati.
Quindi non ci sono intersezioni nel piano euclideo.
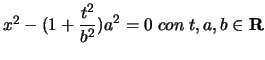 . Questo ci dice che qualunque sia
. Questo ci dice che qualunque sia 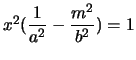 quindi:
quindi:
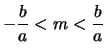 ,
,
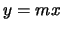 taglia
taglia 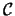 in due punti distinti
in due punti distinti
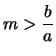 oppure
oppure
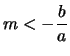 ,
,
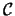 in due punti complessi e coniugati,
quindi non la interseca nel piano euclideo.
in due punti complessi e coniugati,
quindi non la interseca nel piano euclideo.
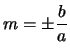 .
.
![\includegraphics[width=9cm,height=7.5cm]{i-regione}](img21.png)