Osservazione 3  

 L'equazione 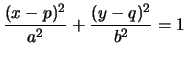$\displaystyle\frac{(x-p)^{2}}{a^{2}}+\frac{(y-q)^{2}}{b^{2}}=1$ rappresenta ancora un'iperbole, tuttavia essa č di centro $C=(p,q)$ e le rette $X=p$, $Y=q$ sono i suoi assi di simmetria.
L'equazione si riduce in forma canonica con la traslazione

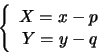
\begin{displaymath} \left \{ \begin{array}{l} X=x-p\\ \, Y=y-q\\ \end{array} \right. \end{displaymath}

Osservazione 4 (Iperbole equilatera)   

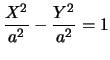La conica $\mathcal{C}: X^{2}-Y^{2}=a^{2}$, ossia $\displaystyle\frac{X^{2}}{a^{2}}-\frac{Y^{2}}{a^2}=1$ ( caso in cui $a=b$ ) prende il nome di iperbole equilatera. Essa ha asintoti di equazione $y=\pm x$, tali rette sono le bisettrici del 1^e 3^ e del 2^ e 4^ quadrante rispettivamente.

Possiamo allora, con opportuno cambiamento di coordinate, assumerli come nuovi assi coordinati. Infatti, ricordando le formule di rotazione

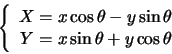
\begin{displaymath} \left \{ \begin{array}{rl} X=x\cos\theta-y\sin\theta\\ Y=x\sin\theta+y\cos\theta \end{array} \right. \end{displaymath}
 

prendiamo $\displaystyle\theta=-\frac{\pi}{4}$, ruotiamo cioč il piano in senso orario di 45^. Avremo allora:

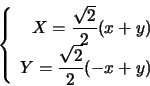
\begin{displaymath} \left \{ \begin{array}{rl} X=\displaystyle\frac{\sqrt{2}}... ...Y=\displaystyle\frac{\sqrt{2}}{2}(-x+y) \end{array} \right. \end{displaymath}

che sostituite nell'equazione ci da
\begin{displaymath} \displaystyle\frac{1}{2}(x+y)^{2}-\frac{1}{2}(-x+y)^{2}=a^{2} \end{displaymath}


e sviluppando

\begin{displaymath} \displaystyle xy=\frac{1}{2}a^{2}\qquad (con \, \, \frac{a^2}{2}>0). \end{displaymath}

Il grafico di $xy=c$, per $c>0$, č il seguente:
Figura: Nel nuovo sistema di riferimento gli assi x ed y sono gli asintoti dell'iperbole equilatera.
\includegraphics[width=9cm,height=7.5cm]{ipequilatera}