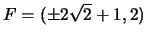Verificare che l'equazione
![]() rappresenta un iperbole, e trovarne centro, asintoti e fuochi.
rappresenta un iperbole, e trovarne centro, asintoti e fuochi.
Soluzione: Basta riscrivere l'equazione nel modo seguente
(metodo del completamento dei quadrati):
cioč:
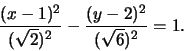
La traslazione
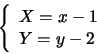
trasforma l'equazione nella seguente:
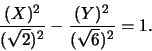
Tale equazione rappresenta un'iperbole.
- rispetto agli assi
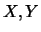 il centro č
il centro č 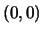 ; gli assi di simmetria sono
; gli assi di simmetria sono 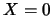 ,
, 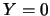 ; i
vertici sono
; i
vertici sono
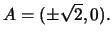 Gli asintoti sono le rette
Gli asintoti sono le rette
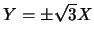 .
.
I fuochi sono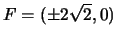
- rispetto agli assi
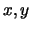 il centro č
il centro č 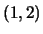 ; gli assi di simmetria sono
; gli assi di simmetria sono 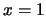 ,
, 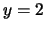 ; i
vertici sono
; i
vertici sono
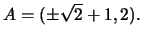 Gli asintoti sono le rette
Gli asintoti sono le rette
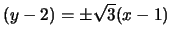 .
.
I fuochi sono