Le coniche sono curve studiate sin dall'antichità e molti
matematici hanno dato il loro contributo allo studio di tali
curve. Sembra che per primo Menecmo
(375-325 a.C.), un matematico
greco maestro di Alessandro Magno, si sia imbattuto nelle coniche
nel tentativo di risolvere uno dei tre famosi problemi della
matematica greca (i problemi di Delo). Egli stava studiando curve
dotate di proprietà adatte alla duplicazione del cubo. Apollonio
(262-190 a.C.), conosciuto come il Grande Geometra, consolidò ed
approfondì i precedenti risultati sulle coniche nell'opera Le
Coniche. Apollonio fu il primo a dimostrare che era possibile
ottenere tutte e tre le sezioni coniche intersecando un cono con
un piano e facendo poi variare l'inclinazione di tale piano. Fu
anche il primo ad attribuire i nomi di ellisse, parabola, ed
iperbole.
Successivamente le leggi di Keplero
sui movimenti dei pianeti
diedero una notevole applicazione delle coniche e delle loro
proprietà geometriche. In termini moderni possiamo dire che ogni
corpo dotato di massa determina intorno a sé una zona di spazio in
cui le altre masse risentono della sua attrazione, un campo
gravitazionale. Un corpo che si muove in un campo gravitazionale,
può descrivere tre diversi tipi di traiettorie: ellittica,
iperbolica o parabolica. Tali traiettorie dipendono dalla velocità
iniziale e dalla direzione del corpo. Nel caso di orbite
ellittiche si parla di traiettoria chiusa (per es. la terra
intorno al sole, la luna intorno la terra). Nel caso di orbite
iperboliche e paraboliche si parla di orbite aperte (per es. una
cometa intorno al sole).
Figura 1.1:
Le coniche descrivono traiettorie possibili
di corpi in interazione gravitazionale
(per es. il sole e la terra, il sole e una cometa).
|
|
Una equazione del tipo 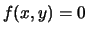 , dove
, dove 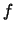 è un polinomio di
secondo grado a coefficienti reali, definisce una curva piana che
si chiama conica. Detta
è un polinomio di
secondo grado a coefficienti reali, definisce una curva piana che
si chiama conica. Detta 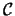 tale conica,
l'equazione generale si scrive:
tale conica,
l'equazione generale si scrive:
Scegliendo un opportuno sistema di coordinate cartesiane,
l'equazione di una conica si può riscrivere in una delle seguenti
forme.
Una conica la cui equazione sia così scritta si dice in
forma canonica; inoltre se i coefficienti sono tutti non
nulli si dice non degenere.
Studieremo ora le coniche in forma canonica enunciando, di volta
in volta, le principali proprietà geometriche di ciascuna di esse.
Inoltre vedremo che possono essere viste come particolari luoghi
geometrici.
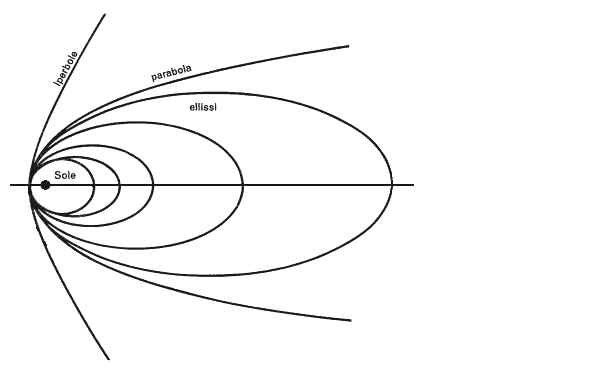

![]() , dove
, dove ![]() è un polinomio di
secondo grado a coefficienti reali, definisce una curva piana che
si chiama conica. Detta
è un polinomio di
secondo grado a coefficienti reali, definisce una curva piana che
si chiama conica. Detta ![]() tale conica,
l'equazione generale si scrive:
tale conica,
l'equazione generale si scrive: