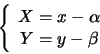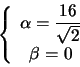Soluzione: Poniamo
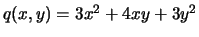 , forma
quadratica che ha come matrice
, forma
quadratica che ha come matrice
Il suo polinomio caratteristico è
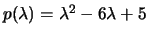 , gli autovalori sono
, gli autovalori sono
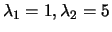 .
Adesso
.
Adesso
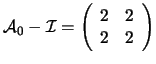 .
Una soluzione del sistema
.
Una soluzione del sistema
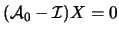 (
(
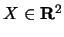 ) è il vettore
) è il vettore
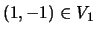 che
normalizzato è
che
normalizzato è
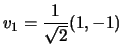 .
Sfruttiamo il fatto che
.
Sfruttiamo il fatto che
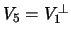 , poi normalizziamo,
allora
, poi normalizziamo,
allora
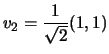 .
.
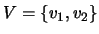 rappresenta una base ortonormale di autovettori
di
rappresenta una base ortonormale di autovettori
di 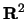 ,
,
Quindi
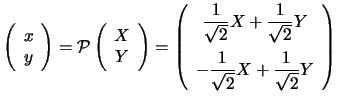 è la trasformazione in coordinate ortonormali da cui si
ottiene:
è la trasformazione in coordinate ortonormali da cui si
ottiene:
semplificando,
Facciamo ora la traslazione
e svolgiamo i calcoli.
Allora
Poniamo ora
da cui si ottiene:
che rappresenta l'equazione canonica di un ellisse.
Figura:
In verde l'ellisse in forma generale,
in rosso l'ellisse i forma canonica
|
|
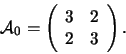
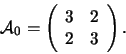
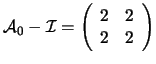 .
Una soluzione del sistema
.
Una soluzione del sistema
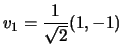 .
Sfruttiamo il fatto che
.
Sfruttiamo il fatto che
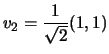 .
.
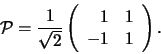
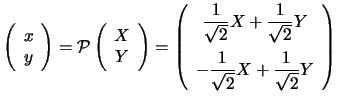 è la trasformazione in coordinate ortonormali da cui si
ottiene:
è la trasformazione in coordinate ortonormali da cui si
ottiene: