


Next: About this document ...
Up: Esercizi
Previous: Esercizi
Date la seguenti coniche scritte in forma generale dire di che
tipo di coniche si tratta:
1.
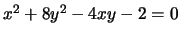
2.
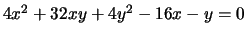
3.
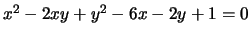
4.
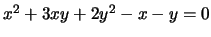 .
.
Soluzione
1.
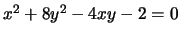
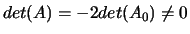 , non degenere
, non degenere
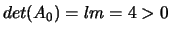 .
.
Gli autovaloi di 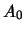 hanno segno concorde e si vede, calcolandoli,
che sono entrambi positivi.
Inoltre
hanno segno concorde e si vede, calcolandoli,
che sono entrambi positivi.
Inoltre
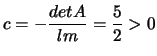 , allora
l'equazione rappresenta un ellisse reale.
, allora
l'equazione rappresenta un ellisse reale.
2.
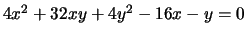
Soluzione
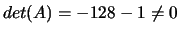 , non degenere,
, non degenere,
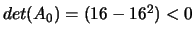 .
.
I due autovalori hanno segno discorde, in più
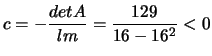 .
Quindi l'equazione che rappresenta la conica in forma canonica è del
tipo:
.
Quindi l'equazione che rappresenta la conica in forma canonica è del
tipo:
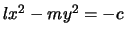 , cioè
, cioè 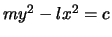 che rappresenta l'equazione di
un'iperbole.
che rappresenta l'equazione di
un'iperbole.
3.
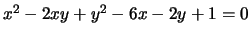
Soluzione
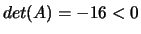 , non degenere.
, non degenere.
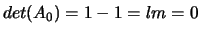 , quindi almeno un autovalore è nullo.
, quindi almeno un autovalore è nullo.
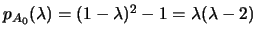 , un autovalore è
nullo allora, poichè abbiamo visto che la conica è non degenere,
l'equazione rappresenta una parabola.
, un autovalore è
nullo allora, poichè abbiamo visto che la conica è non degenere,
l'equazione rappresenta una parabola.
4.
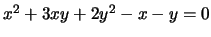
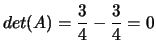 , degenere.
, degenere.
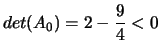 , due autovalori non nulli che
hanno segno discorde,
, due autovalori non nulli che
hanno segno discorde, 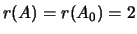 . Si vede , dalla lista del
Teorema 1 che la forma canonica sarà del tipo
. Si vede , dalla lista del
Teorema 1 che la forma canonica sarà del tipo 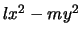 che
rappresenta l'unione di due rette incidenti in un punto.
che
rappresenta l'unione di due rette incidenti in un punto.



Next: About this document ...
Up: Esercizi
Previous: Esercizi
Claudio Benizi
2002-10-14
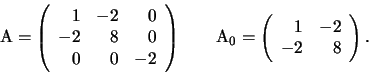
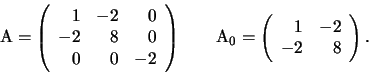
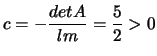 , allora
l'equazione rappresenta un ellisse reale.
, allora
l'equazione rappresenta un ellisse reale.
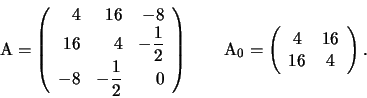
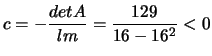 .
Quindi l'equazione che rappresenta la conica in forma canonica è del
tipo:
.
Quindi l'equazione che rappresenta la conica in forma canonica è del
tipo:
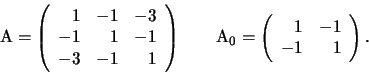
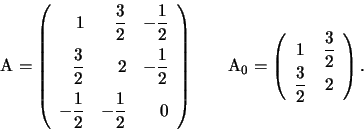
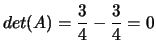 , degenere.
, degenere.
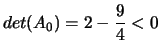 , due autovalori non nulli che
hanno segno discorde,
, due autovalori non nulli che
hanno segno discorde,