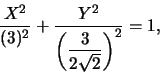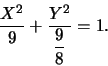L'equazione
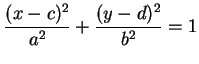 è
ancora un'ellisse, tuttavia essa è di centro C=(c,d) e le rette
è
ancora un'ellisse, tuttavia essa è di centro C=(c,d) e le rette
L'equazione si riduce in forma canonica con la traslazione
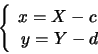
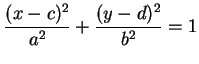 è
ancora un'ellisse, tuttavia essa è di centro C=(c,d) e le rette
è
ancora un'ellisse, tuttavia essa è di centro C=(c,d) e le rette
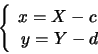
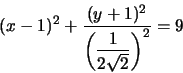
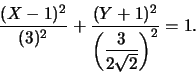
La curva in questione è un'ellisse. Da qui il centro è in
![]() e i semiassi sono le rette
e i semiassi sono le rette
![]() ,
, ![]() ;
;
le lunghezze dei semiassi sono rispettivamente ![]() ,
,
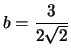 ;
;
![]() dunque i fuochi stanno sull'asse orizzontale.
dunque i fuochi stanno sull'asse orizzontale.
La traslazione
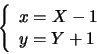
trasforma l'equazione nella seguente: