Simmetrie.
Se 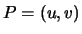 appartiene a
appartiene a 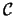 , questa contiene anche i
punti
, questa contiene anche i
punti
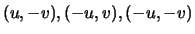 . Infatti le variabili
. Infatti le variabili 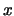 e
e 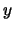 compaiono soltanto al quadrato, quindi l'ellisse è una curva
simmetrica, sia rispetto l'asse
compaiono soltanto al quadrato, quindi l'ellisse è una curva
simmetrica, sia rispetto l'asse 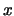 , sia rispetto all'asse
, sia rispetto all'asse 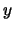 ,
e quindi anche simmetrica rispetto all'origine.
Se
,
e quindi anche simmetrica rispetto all'origine.
Se 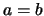 , cioè se
, cioè se 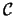 è una circonferenza di
centro l'origine e raggio
è una circonferenza di
centro l'origine e raggio 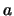 , ogni asse per l'origine
é asse di simmetria.
, ogni asse per l'origine
é asse di simmetria.