Regione in cui si trova la curva.
L'equazione dell'ellisse si può anche scrivere nel modo seguente:
Poichè
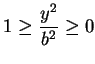 i valori di
i valori di
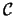 lungo l'asse
lungo l'asse 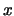 variano tra
variano tra 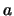 e
e 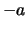 ;
analogamente le
;
analogamente le 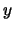 variano tra
variano tra 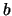 e
e 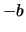 . Allora il grafico
dell'ellisse è contenuto nell'insieme costituito dai punti
. Allora il grafico
dell'ellisse è contenuto nell'insieme costituito dai punti
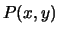 del piano tali che
del piano tali che 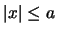 ,
, 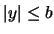 , cioè nel
rettangolo delimitato dalle rette di equazioni
, cioè nel
rettangolo delimitato dalle rette di equazioni
I punti di coordinate 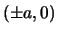 e
e 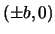 sono i punti di
intersezione di
sono i punti di
intersezione di 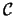 con gli assi cartesiani. Tali punti
si chiamano vertici
dell'ellisse.
con gli assi cartesiani. Tali punti
si chiamano vertici
dell'ellisse.
Figura:
La regione delimitata dalle rette è
la regione dove si svolge il grafico.
|
|
![\begin{displaymath}
x^{2}=a^{2}[1-\displaystyle\frac{y^{2}}{b^{2}}]
\end{displaymath}](img5.png)
![\begin{displaymath}
x^{2}=a^{2}[1-\displaystyle\frac{y^{2}}{b^{2}}]
\end{displaymath}](img5.png)
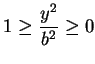 i valori di
i valori di