


Next: About this document ...
se  e
e  hanno lo stesso segno abbiamo invece
hanno lo stesso segno abbiamo invece
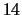 che ammette una sola soluzione reale, per
che ammette una sola soluzione reale, per 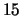 .
Tale polinomio infatti non è riducibile in
.
Tale polinomio infatti non è riducibile in 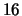 e può
essere fattorizzato nel prodotto di due polinomi di primo grado
nel campo complesso
e può
essere fattorizzato nel prodotto di due polinomi di primo grado
nel campo complesso
 ; la conica quindi è data
dall'unione di due rette di equazione
; la conica quindi è data
dall'unione di due rette di equazione  .
.
L'equazione rappresenta una coppia di rette complesse coniugate
incidenti in un punto reale, l'origine degli assi.
Per quanto riguarda l'equazione (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) è sufficiente
porre
) è sufficiente
porre
 e si ha
l'equazione canonica di una parabola.
e si ha
l'equazione canonica di una parabola.
Resta soltanto l'equazione (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
)
- Se
 si ottiene l'equazione
si ottiene l'equazione  , cioè una
retta contata due volte. Se
, cioè una
retta contata due volte. Se  rappresenta l'asse Y,
l'equazione
rappresenta l'asse Y,
l'equazione  rappresenta l'asse
rappresenta l'asse  con molteplicità
con molteplicità  .
.
Figura:
l'asse  percorso nei due versi, positivo e negativo.
percorso nei due versi, positivo e negativo.
|
|
Claudio Benizi
2002-10-08
 e si ha
l'equazione canonica di una parabola.
e si ha
l'equazione canonica di una parabola.