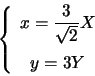Abbiamo visto che, data una conica scritta in forma generale è possibile ridurla, tramite un opportuno cambiamento di coordinate, in una forma più semplice. In questo caso abbiamo effettuato una RIDUZIONE A FORMA CANONICA EUCLIDEA, in quanto abbiamo effettuato un cambiamento di riferimento ortonormale. Invece per una RIDUZIONE A FORMA CANONICA AFFINE si procede allo stesso modo, tuttavia si tiene conto del fatto che i cambiamenti di coordinate ammissibili sono di tipo affine quindi, per esempio, l'equazione dell'esempio 2 può essere semplificata ulteriormente mediante il cambiamento di coordinate (non ortogonale)