In ![]() classificare la conica di
equazione
classificare la conica di
equazione
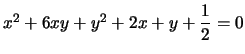 .
.
Soluzione: La parte quadratica dell'equazione è
![]() e la sua matrice associata è
e la sua matrice associata è
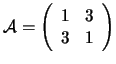 .
.
![]() è il polinomio
caratteristico con radici
è il polinomio
caratteristico con radici ![]() ,
, ![]() , allora
, allora
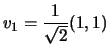 ,
,
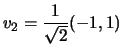 è una base ortonormale
di autovettori. La matrice del cambiamento di coordinate è
è una base ortonormale
di autovettori. La matrice del cambiamento di coordinate è
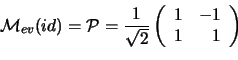 , che ci permette di ottenere una forma diagonale di
, che ci permette di ottenere una forma diagonale di
![]() . Consideriamo quindi la seguente trasformazione di
coordinate ortonormali:
. Consideriamo quindi la seguente trasformazione di
coordinate ortonormali:
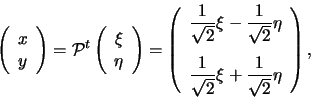
essa trasformerà l'equazione data in
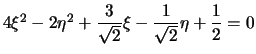 .
Vediamo ora come eliminare i termini di
.
Vediamo ora come eliminare i termini di ![]() grado. Facciamo
la traslazione
grado. Facciamo
la traslazione
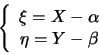
Se poniamo
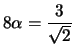 ,
,
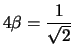 e facciamo un po' di
calcoli, abbiamo che con la traslazione:
e facciamo un po' di
calcoli, abbiamo che con la traslazione:
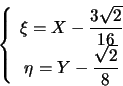
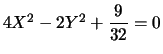 cioè:
cioè:
che è l'equazione di un' iperbole con asse focale l'asse delle Y.
![\includegraphics[width=9cm,height=20cm]{es2iperbole.eps}](img22.png)