In ![]() , data la curva di equazione
, data la curva di equazione
![]() ,
trovare di che tipo di conica si tratta.
,
trovare di che tipo di conica si tratta.
Soluzione: Posto
![]() , essa è una forma
quadratica che ha come matrice
, essa è una forma
quadratica che ha come matrice
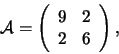
![]() . Il polinomio caratteristico di
. Il polinomio caratteristico di ![]() è
è
![]() con autovalori
con autovalori
![]() .
Adesso, poichè
.
Adesso, poichè
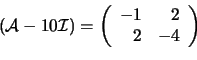 , risolviamo il sistema
, risolviamo il sistema
![]() , con
, con
![]() , e troviamo
che il vettore
, e troviamo
che il vettore
![]() (dove
(dove ![]() è autospazio
relativo all'autovalore
è autospazio
relativo all'autovalore ![]() ); normalizziamo, e abbiamo
che
); normalizziamo, e abbiamo
che
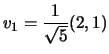 . Per trovare l'altro
autovettore basterà risolvere il sistema precedente con
. Per trovare l'altro
autovettore basterà risolvere il sistema precedente con
![]() oppure sfruttare il fatto che
oppure sfruttare il fatto che
![]() , poi
normalizzare, allora
, poi
normalizzare, allora
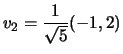 .
.
![]() rappresenta una base ortonormale di autovettori
di
rappresenta una base ortonormale di autovettori
di ![]() . Consideriamo
. Consideriamo
![]() e
e
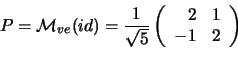 la matrice del cambiamento di base dalla base canonica di
la matrice del cambiamento di base dalla base canonica di
![]() alla base
alla base ![]() ; siano poi
; siano poi ![]() coordinate di
coordinate di
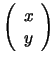 rispetto a
rispetto a ![]() .
. ![]() è ortogonale, cioè tale che
è ortogonale, cioè tale che
![]() . Quindi
. Quindi
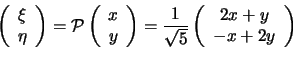 ; allora la forma quadratica associata sarà:
; allora la forma quadratica associata sarà:
Riassumendo, siamo partiti dalla curva di equazione
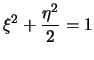 che è l'equazione di un ellisse. Inoltre i suoi assi di simmetria
sono
che è l'equazione di un ellisse. Inoltre i suoi assi di simmetria
sono ![\includegraphics[width=5.5cm,height=7cm]{es1assi.ps}](img32.png)
![\includegraphics[width=6cm,height=17cm]{es1ellisse.eps}](img33.png)