DIMOSTRAZIONE

Per le proprietà del logaritmo è evidente che

logn! = log1 + log2 + ........... + logn

Poichè logx è una funzione monotona crescente di x si ha la seguente disuguaglianza:

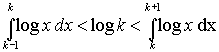
Sommando per k = 1, ........., n si ha che:

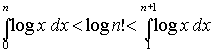
Risolvendo gli integrali si ottiene la seguente stima di logn!:

nlogn – n < logn! < (n + 1)log(n + 1) - n

Si consideri ora la successione

Si può verificare che

e che

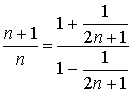
Pertanto

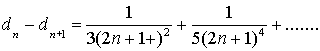
La successione d_n è, quindi, strettamente decrescente e

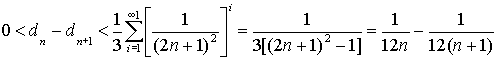
Per quest’ultima disuguaglianza si può affermare che la successione

è strettamente crescente, quindi esiste ed è finito il limite per le due successioni considerate

(uguali per entrambe).

Indicando tale limite con L, si può concludere che

Per dimostrare quest’ultima cosa si possono utilizzare alcuni risultati riguardanti la distribuzione gaussiana.

Ciò non rientra però negli scopi di tale presentazione.