SOLUZIONE 4

a) Il numero di modi di formare un Pin è 10⁵ perchè per

ogni cifra abbiamo 10 possibilità.

b) Il numero di modi di formare un Pin con cifre tutte

diverse è equivalente al numero di modi di scegliere 5

elementi su 10 tenendo conto dell’ordine e senza

ripetizione:

c) Il numero di modi di formare un Pin se la prima

cifra deve essere diversa da 0 è

Infatti per la prima cifra abbiamo solo 9 possibili scelte

in quanto si è escluso lo 0 ma per tutte le altre ne

abbiamo 10.

d) Il numero di modi di formare un Pin con cifre

tutte diverse se la prima cifra non può essere lo 0 è

Infatti per la prima cifra abbiamo 9 possibili scelte perchè

basta che sia diversa dallo 0.

Per quanto riguarda la seconda abbiamo ancora 9 possibili

scelte perchè deve essere diversa dalla prima.

La terza deve essere diversa sia dalla prima che dalla

seconda, quindi restano 8 possibili numeri da poter

scegliere e così via fino alla quinta cifra.

e) Il numero di modi di formare un Pin con esattamente

2 cifre uguali se la prima è diversa da 0 è

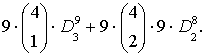
Infatti si possono presentare 2 casi.

Primo caso

Una delle 2 cifre uguali è la prima per la quale si hanno 9

possibili scelte.

Il numero di modi di scegliere, fra le restanti 4 cifre, quella

uguale alla prima è:

Per le restanti 3 cifre le possibili scelte sono, rispettivamente

9, 8 e 7.

Da qui deriva il primo termine del risultato.

Secondo caso

Tra le due cifre uguali non c’è la prima.

Quindi per la prima cifra si hanno 9 possibili scelte

(deve essere diversa da 0).

Il numero di modi possibili di scegliere, fra le restanti 4

cifre, le 2 uguali è:

Per le 2 restanti cifre si hanno rispettivamente 8 e 7

possibilità.

Da qui deriva il secondo termine del risultato.

Sommando si ottiene:

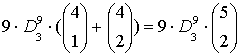
Infatti si può anche pensare di scegliere le 2 uguali

sulle 5 e poi si avrà:

- 9 possibili scelte per la prima.

- 9 scelte per le 2 uguali.

essere diverse.