Definizione 2 : r-disposizioni semplici
Le r-disposizioni
semplici sono il numero di funzioni iniettive da un insieme di r
elementi ad uno di
n
elementi.
Esse
equivalgono al caso in cui gli r elementi vengono scelti TENENDO
CONTO
DELL’ORDINE
e SENZA
RIPETIZIONE.
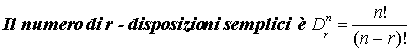
Infatti
in questo caso, visto che non sono ammesse le ripetizioni, abbiamo la seguente
situazione:
1° elemento ® n scelte
2° elemento ® n - 1 scelte
................................................
r-esimo elemento ® n – (r – 1)
scelte
Quindi in
totale si hanno n( n – 1
)( n – 2 )........... ( n – r + 1 ) possibilità.
Questo
prodotto viene indicato di solito in questo modo:
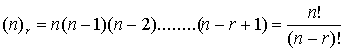
Esempio 2: Riprendiamo l’esempio fatto
per le disposizioni: si vogliono scegliere 2 elementi
dall’insieme { 1 , 2 , 3 } tenendo conto dell’ordine.
( 1 , 1 ) ( 1 , 2 ) ( 1 , 3 )
( 2 , 1 ) ( 2 , 2 ) ( 2 , 3 )
( 3 , 1 ) ( 3 , 2 ) (
3 , 3 )
Le
disposizioni semplici risultano essere 6 = (n)r con n
= 3 e r = 2.
Nel caso
particolare in cui n = r si ottengono le permutazioni
di n elementi che indicano i modi in
cui essi possono essere
ordinati.
Il numero totale delle
permutazioni di n elementi è n!.


