Prima di spiegare le regole fondamentali del calcolo combinatorio, è necessario rivedere la definizione

e le proprietà del coefficiente binomiale.

Esso riveste infatti un ruolo molto importante in teoria della probabilità.

Definizione : Dati m ed n numeri naturali, si definisce il coefficiente binomiale per

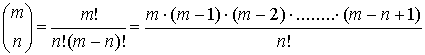
PROPRIETÀ DEL BINOMIALE

Le seguenti proprietà derivano evidentemente dalla definizione precedente.

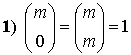
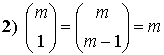
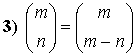
Meno evidente ma altrettanto semplice da dimostrare è la

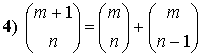
Essa si verifica sommando i due termini a destra dopo averli esplicitati.

L’ultima formula ci permette di calcolare il coefficiente binomiale per induzione su m; infatti

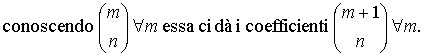
Una maniera rapida di eseguire questo calcolo è scrivere il triangolo di Tartaglia:

...............................................

In tal caso si ha che la m-esima riga è formata dai seguenti m coefficienti:

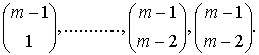
La proprietà 4) ci assicura che un elemento di una riga che non sia né il primo né l’ultimo risulta

essere la somma dei due che sono sopra di esso.

Ogni riga può essere costruita a partire dalle precedenti, mettendo al primo e all’ultimo posto 1

Il triangolo di Tartaglia è più noto nella forma

1

1 1

\ /

1 2 1

\ / \ /

1 3 3 1

\ / \ / \ /

1 4 6 4 1

....................................................