In questa appendice si presenta un’ulteriore dimostrazione della formula di Stirling.

  Quella che verrà esposta qui di seguito vuole verificare che

 

 

  Di fondamentale importanza ai fini di questa dimostrazione è la funzione gamma di Eulero così definita:

 

 

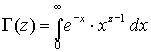
  Si ha che

 

 

 

 

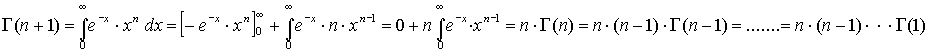
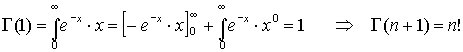
  La funzione gamma di Eulero può anche essere scritta nel seguente modo:

 

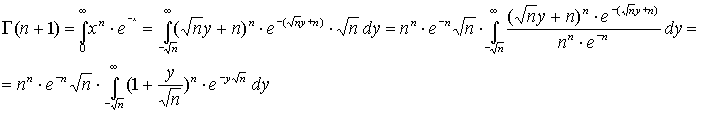
  Questo integrale può essere spezzato così:

 

 

 

 

 

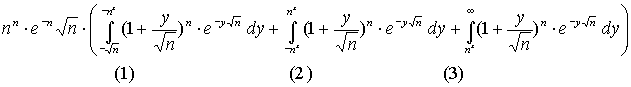
  2)  Si considera ancora il logaritmo della funzione integranda e se ne fa lo sviluppo di Taylor:

 

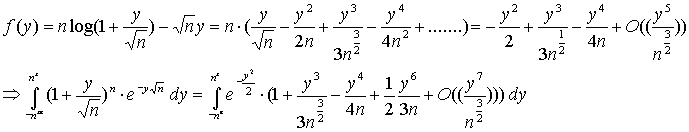
  I termini di grado dispari sono pari a 0 perché l’integrale di una funzione dispari su un dominio simmetrico è nullo.

  Gli integrali nella parentesi tendono ai momenti centrati della gaussiana, che sono finiti.

 

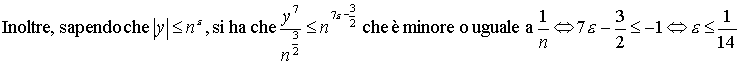
  ne segue che

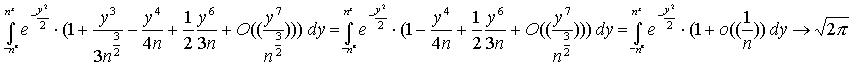
  per le proprietà della gaussiana.

 

3)     Considerando la f (y) vista sopra si ha che:

 

 

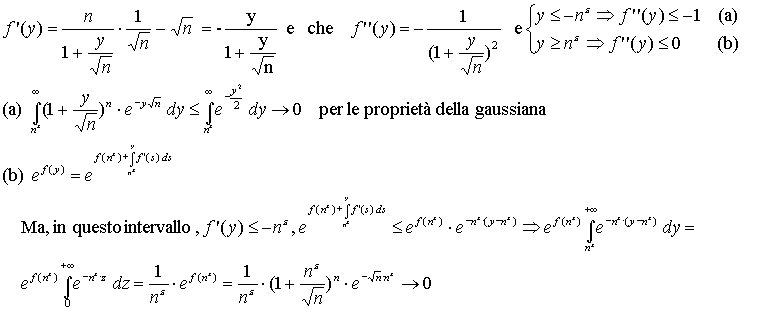
  Si è ottenuta così la formula.

  In questa dimostrazione si è approssimata la funzione integranda della gamma di Eulero con una gaussiana.

 

  Questo si può vedere graficamente CLICCANDO QUI.