Si consideri il campo
K (ad esempio
K = R , C ).
Siano A e B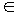 M n,n(K).
M n,n(K).
Si possono dimostrare le seguenti proprietÓ del
determinante:
 |
Se A ha due righe (o colonne) uguali, oppure una riga (o colonna) di zero,
allora det A=0. |
 |
det (A .B) = det A . det B
Teorema di Binet |
|
 |
Se A' Ŕ la matrice ottenuta da A scambiando di posto due
colonne o due righe, allora
det A' = _ det A.
|
 |
det tA = det A |
|
 |
det A non cambia se in
A sommiamo ad una riga (o ad una colonna) una
combinazione lineare delle altre righe (o colonne). |
 |
det (A+B) e det A + det B sono diversi
ATTENZIONE! |
|
 |
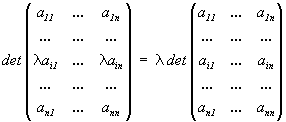
|
|

|
Indice
|
|



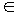 M n,n(K).
M n,n(K).