|
Si consideri il campo
K (ad esempio
K = R , C ). Siano A e B 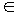 M n,n(K).
M n,n(K).Si possono dimostrare le seguenti proprietÓ del determinante:
| ||||||||||||||||||||||||
|
Si consideri il campo
K (ad esempio
K = R , C ). Siano A e B 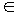 M n,n(K).
M n,n(K).Si possono dimostrare le seguenti proprietÓ del determinante:
| ||||||||||||||||||||||||