Dimostrazione
Sia | 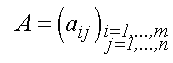 | . |
Una n-upla (x1,...,xn) è soluzione del
sistema Ax = B se e solo se si ha
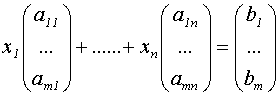
La formula precedente esprime la condizione che il vettore B sia combinazione lineare
delle colonne di A.
Questa condizione è verificata se e solo se la matrice A , B
ha lo stesso rango per colonne di A, cioè se e solo se
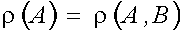
La prima parte del teorema è dimostrata.
Se 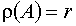 possiamo supporre che le sue prime r equazioni
siano linearmente indipendenti e sostituire il sistema Ax = B possiamo supporre che le sue prime r equazioni
siano linearmente indipendenti e sostituire il sistema Ax = B
con il sistema equivalente:
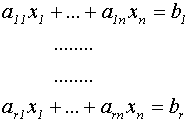
Applicando il metodo di eliminazione di Gauss a quest'ultimo sistema, nessuna
delle equazioni si riduce a 0 = 0 perchè ciò implicherebbe che essa è linearmente dipendente da
quelle che la precedono.
Quindi il sistema Ax = B si può trasformare in un sistema a gradini di r equazioni.
Ciò significa che l'ultimo sistema, e quindi Ax = B , possiede
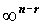 soluzioni. soluzioni.
|
 |
Indice |
|


