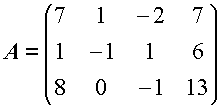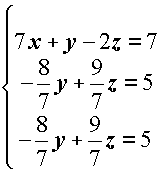Si consideri il sistema 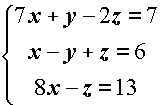 ; ; |
| La matrice associata al sistema è la matrice |
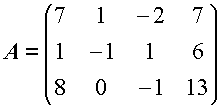 |
Usando il metodo di eliminazione di Gauss,
si riduce  nella forma nella forma
|
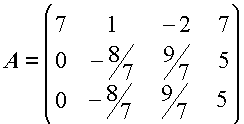
|
|
Il sistema di partenza è equivalente al seguente:
|
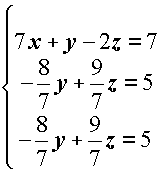
|
possiede cioè le stesse soluzioni. |
|
Ora:
 Le ultime due equazioni sono uguali: ciò significa che una delle due deve essere eliminata, poichè non aggiunge informazioni a quelle già fornite.
Non si consideri, ad esempio, la terza. Le ultime due equazioni sono uguali: ciò significa che una delle due deve essere eliminata, poichè non aggiunge informazioni a quelle già fornite.
Non si consideri, ad esempio, la terza.
 Dalla seconda equazione posso ricavare, indifferentemente, la variabile z o
la variabile y :
in ogni caso si ottiene una variabile in funzione dell'altra.
Dalla seconda equazione posso ricavare, indifferentemente, la variabile z o
la variabile y :
in ogni caso si ottiene una variabile in funzione dell'altra.
|
 Sia, ad esempio,
Sia, ad esempio, 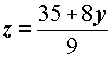 .
In questo caso, y è la
variabile libera. .
In questo caso, y è la
variabile libera.
Dalla prima equazione
si ricava facilmente la variabile x, anch'essa in funzione di y :
 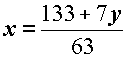
 La soluzione è rappresentata dal vettore La soluzione è rappresentata dal vettore 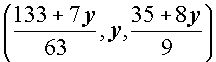 . .
Il sistema è dunque
indeterminato, poichè al variare di y si ottengono infinite (
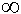 1 ) soluzioni diverse. 1 ) soluzioni diverse.
|

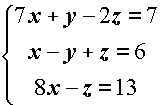 ;
;