SULL'EQUILIBRIO DEI PIANI OVVERO : SUI CENTRI DI GRAVITA' DEI PIANI.
Quest'opera è composta da due libri.
Descrive la legge di equilibrio delle leve e determina le aree e il centro di gravità (baricentro) di varie figure geometriche. Potremmo quindi definirlo un trattato di statica.
Questo, tuttavia, non è il più antico testo di fisica: Aristotele, infatti, quasi un secolo prima, aveva pubblicato un'opera intitolata appunto Fisica . Nonostante ciò, c'è una notevole differenza tra le due opere: In Archimede, infatti, lo sforzo è quello di trattare gli argomenti in maniera matematizzata, aspetto quasi assente nell'illustre filosofo.
Vediamo il contenuto di questi due libri.
Il primo libro si concentra sul principio di equilibrio della leva e sullo studio dei baricentri del triangolo e del trapezio. Archimede non fu certamente il primo studioso a occuparsi di questo strumento (già noto da tempo anche all'epoca) e neanche il primo a enunciarne i principi generali. E' sicuro però che il suo punto di vista nello studio di questo oggetto e il suo modo di esprimersi sui risultati ottenuti è a dir poco unico per il suo tempo.
Per una definizione semplice ma accurata della leva, si consiglia la visione del sito di Wikipedia:
http://it.wikipedia.org/wiki/Leva_%28fisica%29
Già in diversi scritti aristotelici si trova il seguente principio:
"Due pesi posti su una bilancia si trovano in equilibrio quando sono inversamente proporzionali alle rispettive distanze dal fulcro.".
Mentre Aristotele dedusse tale principio da ragionamenti cinematici, Archimede lo dedusse da ragionamenti statici. Infatti osservò che
"corpi a simmetria bilaterale sono in equilibrio."
Proviamo a ripercorrere la sua analisi.
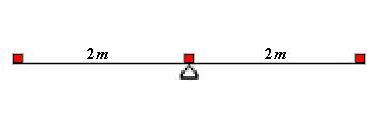
Supponiamo che una sbarra ideale lunga 4m (4 metri) sostenga tre pesi da 1kg ognuno (uno al centro e uno per estremo) e sia in equilibrio su un fulcro posto nel centro, come in figura.
Se partiamo dal postulato archimedeo di simmetria, il sistema è in equilibrio. Però tale principio ci dice di più. Considero solo la parte destra del sistema: se i due pesi (distanti 2m) vengono avvicinati nel punto medio del braccio destro, permane l'equilibrio.
Quindi si deduce che un peso di 1kg sostiene un peso di 2kg nell'altro braccio se il fulcro della leva è a 2m dal peso unitario e a 1m dall'altro peso.
Archimede rimase in ogni caso molto affascinato dalla leva, tanto da utilizzarla in numerose sue invenzioni e macchine da guerra. Era così sicuro della sua conoscenza di questo strumento che è divenuta celebre la sua massima:
"Datemi un punto di appoggio e vi solleverò il mondo."
Nel Medioevo in fisica verranno uniti i punti di vista statico di Archimede e dinamico di Aristotele, ottenendo così vari risultati dal punto di vista scientifico-matematico.
Anche per lo studio del baricentro (concetto già noto anche all'epoca) si deve ad Archimede il contributo necessario a crearne una descrizione accurata e scientifica, come si vedrà meglio nel secondo libro.
Nel secondo libro, troviamo lo studio del centro di massa di una parabola sfruttando il principio di ESAUSTIONE.
Tale metodo permette di calcolare una grandezza tramite "approssimazioni sempre più precise". Un esempio è il calcolo dell'area di una superficie curva (come un segmento di parabola, in figura) che si approssima tramite rettangoli che mi permettano una stima in eccesso e/o in difetto.
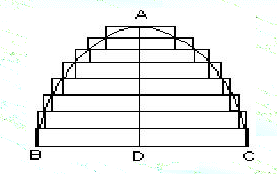
All'aumentare del numero di questi rettangoli, migliorerà la precisione con cui la figura data dai rettangoli si avvicina a quella della parabola.
Questo metodo di ragionamento sarà poi ripreso da Leibniz nel 1600 ed è alla base del calcolo degli integrali nel calcolo infinetesimale.
Inoltre, Archimede studiò il baricentro di un segmento di parabola e, sempre grazie al principio di esaustione, dimostrò che tale centro è situato sul diametro del segmento e divide questo diametro in segmenti che stanno nel rapporto di 3 a 2.
Un altro esempio dell'utilizzo di tale metodo di esaustione riguarda la determinazione dell'area del cerchio. Cerchiamo di analizzarla nei dettagli.
Supponiamo di avere un cerchio di raggio r e circonferenza C e di voler dimostrare che la sua area è 
.
Cominciamo a vedere intuitivamente come potremmo calcolare tale area. Utilizzando il metodo di esaustione, potrei pensare di inscrivere nel mio cerchio un poligono regolare a sua volta divisibile in triangoli uguali, che sapremmo trattare senza problemi:
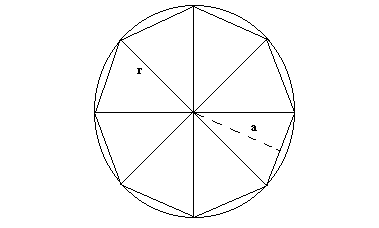
L'area del poligono, infatti, è semplicemente l'area dei triangoli che lo compongono, che potremmo, per maggiore semplicità visiva, rappresentare nelle seguenti forme equivalenti:
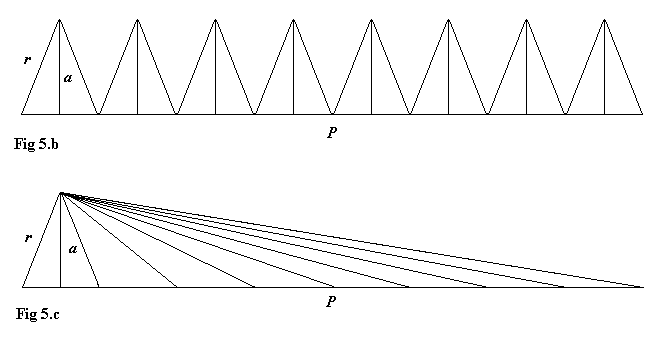
Da cui deduciamo che se indichiamo con P il perimetro del poligono e con a l'altezza dei triangoli, otteniamo che l'area del mio poligono è esattamente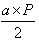 
.
Aumentando il numero dei lati del poligono fino ad ottenere un poligono di infiniti lati, ognuno di lunghezza infinitesima, l'area del poligono e quella del cerchio saranno sempre più simili e si equivarranno quando a coinciderà esattamente con r e P con C.
Cerchiamo, ora,
di fare un piccolo passo avanti e di rendere un po’ più
rigorosa la nostra idea. In particolare, potremmo cercare di effettuare
una dimostrazione per assurdo. Questo ci pone in un'ottica
leggermente diversa: non dobbiamo più dimostrare che l'area del
cerchio è data dalla formula 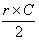, ma dobbiamo mostrare che essa non può essere diversa da .
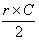Ragioniamo in questo modo:
indicando con A=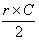
e con D l'area del cerchio, devo arrivare alla conclusione che sia
assurdo che D sia maggiore di A e, analogamente, che ne sia minore. Da
cui non ci resterà che affermare che D coincide esattamente con
A, che era proprio quello che volevamo.
Analizziamo i due casi separatamente:
L'unica conclusione possibile, allora, risulta la nostra di partenza e cioè che l'area del cerchio è esattamente uguale ad A, risultato a cui siamo arrivati proprio grazie al principio di esaustione
Facciamo un latro piccolo passo in avanti e andiamo a definire in maniera rigorosa quanto detto sopra.
Sia sempre A l'area del cerchio. Vogliamo dimostrare che si cade in un assurdo se si suppone che esista un intero positivo k tale che:
Infatti, consideriamo un poligono regolare, inscritto nel nostro cerchio, il cui apotema a sia maggiore di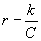 
(tale poligono esiste sempre perché, come abbiamo osservato, posso aumentare il numero di lati fino ad ottenere a = r) inoltre supponiamo che il perimetro P del nostro poligono sia maggiore di 
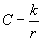(ancora possibile perché aumentando la lunghezza dei lati posso ottenere P = C ).
L'area del poligono è A'=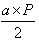, quindi avremo
quindi
che è in contraddizione con
Analogamente per vedere che l'area del cerchio non è maggiore di 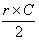, questa volta, però, considerando un poligono circoscritto al cerchio.
